已知椭圆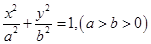 的离心率为
的离心率为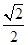 ,且过点
,且过点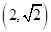

(1)求椭圆的标准方程:
(2)四边形ABCD的顶点在椭圆上,且对角线AC,BD过原点O,若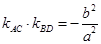
①求 的最值:
的最值:
②求证:四边形ABCD的面积为定值.
已知函数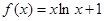
(1)求函数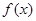 在
在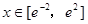 上的最大值与最小值;
上的最大值与最小值;
(2)若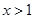 时,函数
时,函数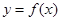 的图像恒在直线
的图像恒在直线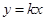 上方,求实数
上方,求实数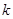 的取值范围;
的取值范围;
(3)证明:当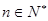 时,
时,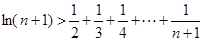
已知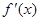 是
是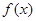 的导函数,
的导函数,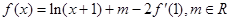 ,且函数
,且函数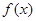 的图象过点
的图象过点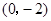 .
.
(1)求函数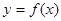 的表达式;
的表达式;
(2)求函数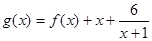 的单调区间和极值.
的单调区间和极值.
已知 ,( a为常数,e为自然对数的底).
,( a为常数,e为自然对数的底).
(1)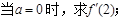
(2)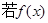
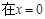 时取得极小值,试确定a的取值范围;
时取得极小值,试确定a的取值范围;
(3)在(2)的条件下,设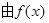 的极大值构成的函数
的极大值构成的函数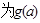 ,将a换元为x,试判断
,将a换元为x,试判断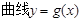 是否能与
是否能与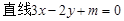 (m为确定的常数)相切,并说明理由.
(m为确定的常数)相切,并说明理由.
设函数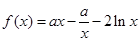 .
.
(1)若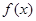 在
在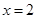 时有极值,求实数
时有极值,求实数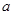 的值和
的值和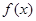 的极大值;
的极大值;
(2)若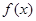 在定义域上是增函数,求实数
在定义域上是增函数,求实数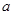 的取值范围.
的取值范围.
已知椭圆C的两焦点分别为 ,长轴长为6,
,长轴长为6,
⑴求椭圆C的标准方程;
⑵已知过点(0,2)且斜率为1的直线交椭圆C于A 、B两点,求线段AB的长度。.