已知
，（ a为常数，e为自然对数的底）．
（1）
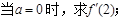
（2）
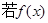
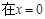时取得极小值，试确定a的取值范围；
（3）在（2）的条件下，设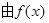
的极大值构成的函数
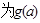，将a换元为x，试判断
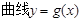是否能与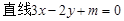
（m为确定的常数）相切，并说明理由．
如图，在四棱锥
中，底面
是直角梯形，侧棱
底面，
垂直于
和
，
是棱
的中点．
（1）求证：
平面
；
（2）求平面与平面
所成的二面角的余弦值；
（3）设点
是直线
上的动点，
与平面所成的角为
，求
的最大值．
已知数列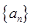
的前
项和为
，向量
满足条件
．
（1）求数列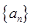的通项公式；
（2）设函数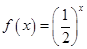
，数列
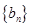满足条件
．
①求数列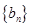的通项公式；
②设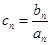
，求数列
的前项和
．
已知函数
.
（1）求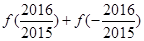
的值；
（2）当
（其中
，且a是常数）时，若
恒成立，求m的取值范围.
如图，在四棱锥
中，底面ABCD为菱形，
，Q为AD的中点，
.
（1）求证：
平面PQB；
（2）点M在线段PC上，
，试确定t的值，使
平面MQB.
如图（1），在三角形ABC中，
，
，点O、M、N分别为线段的中点，将ABO和MNC分别沿BO，MN折起，使平面ABO与平面CMN都与底面OMNB垂直，如图（2）所示.
（1）求证：
平面CMN；
（2）求点M到平面CAN的距离.