如图，在四棱锥
中，底面
是直角梯形，侧棱
底面，
垂直于
和
，
是棱
的中点．
（1）求证：
平面
；
（2）求平面与平面
所成的二面角的余弦值；
（3）设点
是直线
上的动点，
与平面所成的角为
，求
的最大值．
已知函数
（1）若函数
的图象在原点处的切线
与函数
的图象相切，求实数k的值；
（2）若对于
，总存在
，且
满足
，其中e为自然对数的底数，求实数k的取值范围．
篮球比赛时，运动员的进攻成功率=投球命中率×不被对方运动员的拦截率。某运动员在距球篮10米（指到篮圈圆心在地面上射影的距离）以内的投球命中率有如下变化：距球篮1米以内（不含1米）为100％．距离球篮x米处，命中率下降至
．该运动员投球被拦截率为
．试求该运动员在比赛时：（结果精确到
）
（1）在三分线（约距球篮6．72米）处的进攻成功率为多少？
（2）在距球篮几米处的进攻成功率最大，最大进攻成功率为多少？
已知等差数列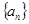
的前n项和为
，
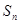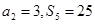，正项数列
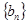满足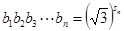
．
（1）求数列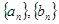
的通项公式；
（2）若
对一切正整数n均成立，求实数
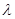的取值范围．
设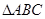
的内角A，B，C的对边分别是
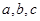，且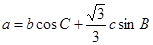
．
（1）求B的大小；
（2）若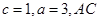
的中点为D，求BD的长．
已知函数
（
）是偶函数．
（1）求实数
的值；
（2）证明：对任意的实数
，函数
的图象与直线
最多只有一个公共点；
（3）设
，若
与
的图象有且只有一个公共点，求实数
的取值范围．