已知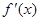 是
是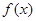 的导函数,
的导函数,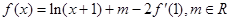 ,且函数
,且函数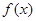 的图象过点
的图象过点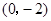 .
.
(1)求函数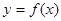 的表达式;
的表达式;
(2)求函数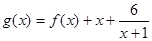 的单调区间和极值.
的单调区间和极值.
(本小题满分12分)
已知二次函数f(x) 对任意x∈R,都有f (1-x)="f" (1+x)成立,设向量a="(sinx,2)," b=(2sinx, ),c=(cos2x,1),d=(1,2)。
),c=(cos2x,1),d=(1,2)。
(1)分别求a·b和c·d的取值范围;
(2)当x∈[0,π]时,求不等式f(a·b)>f(c·d)的解集。
(本小题满分12分)
设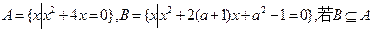 ,求实数
,求实数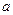 的取值范围。
的取值范围。
(本小题共l5分) 如图,在直三棱柱ABC-A1B1C1中.∠ BAC=90°,AB=AC=AA1 =1.D是棱CC1上的一点,P是AD的延长线与A1C1的延长线的交点,且PB1∥平面BDA1.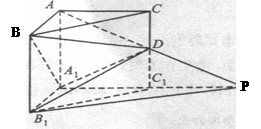
(I)求证:CD=C1D:
(II)求二面角A-A1D-B的平面角的余弦值;
(Ⅲ)求点C到平面B1DP的距离.
(本小题满分12分)口袋中有质地、大小完全相同的5个球,编号分别为1,2,3,4,5,甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,如果两个编号的和为偶数算甲赢,否则算乙赢.
(1)求甲赢且编号的和为6的事件发生的概率;
(2)这种游戏规则公平吗?试说明理由.
(本小题满分12分)如图,四边形ABCD为正方形,QA⊥平面ABCD,PD∥QA,QA=AB=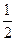 PD.
PD.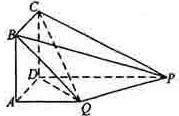
(I) 证明:PQ⊥平面DCQ;
(II)求棱锥Q—ABCD的的体积与棱锥P—DCQ的体积的比值.