(本小题满分14分)已知椭圆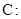
 (
(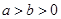 )的离心率为
)的离心率为 ,右焦点
,右焦点 到直线
到直线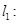
 的距离为
的距离为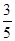 .
.
(1)求椭圆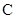 的标准方程;
的标准方程;
(2)过椭圆右焦点 ,斜率为
,斜率为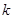 (
( )的直线
)的直线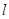 与椭圆
与椭圆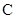 相交于
相交于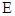 、
、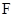 两点,
两点,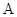 为椭圆的右顶点,
为椭圆的右顶点,
直线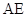 ,
,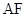 分别交直线
分别交直线 于点
于点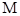 ,
, ,线段
,线段 的中点为
的中点为 ,记直线
,记直线 的斜率为
的斜率为 ,求证:
,求证: 为定值.
为定值.
如图四棱锥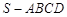 ,底面四边形ABCD满足条件
,底面四边形ABCD满足条件 ,
, ,侧面SAD垂直于底面ABCD,
,侧面SAD垂直于底面ABCD, ,
,
(1)若SB上存在一点E,使得 平面SAD,求
平面SAD,求 的值;
的值;
(2)求此四棱锥体积的最大值;
(3)当体积最大时,求二面角A-SC-B大小的余弦值.
将数列{an}中的所有项按每一行比上一行多一项的规则排成如下数表:
a1
a2a3
a4a5 a6
a7 a8 a9a10
……
记表中的第一列数a1,a2,a4,a7,…构成的数列为{bn},b1=a1="1." Sn为数列{bn}的前n项和,且满足 =1(n≥2).
=1(n≥2).
(Ⅰ)证明数列{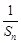 }成等差数列,并求数列{bn}的通项公式;
}成等差数列,并求数列{bn}的通项公式;
(Ⅱ)上表中,若从第三行起,每一行中的数按从左到右的顺序均构成等比数列,且公比为同一个正数.当 时,求上表中第k(k≥3)行所有项的和.
时,求上表中第k(k≥3)行所有项的和.
已知向量 ,
, ,函数
,函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)在
 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
, ,且
,且 ,求
,求 的值.
的值.
(本小题满分14分)已知函数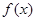 定义在区间
定义在区间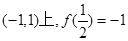 ,对任意
,对任意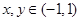 ,恒有
,恒有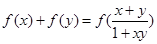 成立,又数列
成立,又数列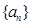 满足
满足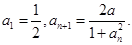 (I)在(-1,1)内求一个实数t,使得
(I)在(-1,1)内求一个实数t,使得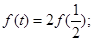 (II)求证:数列
(II)求证:数列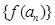 是等比数列,并求
是等比数列,并求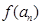 的表达式;(III)设
的表达式;(III)设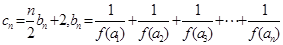 ,是否存在
,是否存在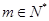 ,使得对任意
,使得对任意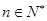 ,
,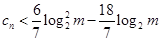 恒成立?若存在,求出m的最小值;若不存在,请说明理由。
恒成立?若存在,求出m的最小值;若不存在,请说明理由。
(本小题满分13分)已知椭圆C的中心在圆点,焦点在x轴上,F1,F2分别是椭圆C的左、右焦点,M是椭圆短轴的一个端点,过F1的直线 与椭圆交于A,B两点,
与椭圆交于A,B两点, 的面积为4,
的面积为4, 的周长为
的周长为 (I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。
(I)求椭圆C的方程;(II)设点Q的坐标为(1,0),是否存在椭圆上的点P及以Q为圆心的一个圆,使得该圆与直线PF1,PF2都相切,若存在,求出P点坐标及圆的方程;若不存在,请说明理由。