已知向量 ,
, ,函数
,函数 .
.
(Ⅰ)求函数 的最小正周期;
的最小正周期;
(Ⅱ)在
 中,
中, 分别是角
分别是角 的对边,且
的对边,且 ,
, ,
, ,且
,且 ,求
,求 的值.
的值.
(本题10分)
若不等式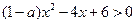 的解集是
的解集是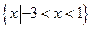 .
.
(1)解不等式 ;
;
(2)b为何值时,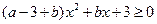 的解集R
的解集R
(本小题满分13分)
已知点F1,F 2为椭圆
2为椭圆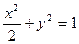 的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线
的两个焦点,点O为坐标原点,圆O是以F1,F2为直径的圆,一条直线 与圆O相切并与椭圆交于不同的两点A,B。
与圆O相切并与椭圆交于不同的两点A,B。
(1)设 的表达式;
的表达式;
(2)若 求直线
求直线 的方程;
的方程;
(3)若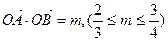 ,求三角形OAB面积的取值范围。
,求三角形OAB面积的取值范围。
(本小题满分13分)
已知函数
(1)求函数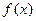 的极值;
的极值;
(2)设函数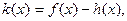 若函数
若函数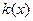 在[1,3]上恰有两个不同零点,求实数a的取值范围。
在[1,3]上恰有两个不同零点,求实数a的取值范围。
(本小题满分13分)
某种有奖销售的饮料,瓶 盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为
盖内印有“奖励一瓶”或“谢谢购买”字样,购买一瓶若其瓶盖内印有“奖励一瓶”字样即为中奖,中奖概率为 甲、乙、丙三位同学每人购买一瓶该饮料。
甲、乙、丙三位同学每人购买一瓶该饮料。
(1)求甲中奖且乙、丙都没有中奖的概率;
(2)求中奖人数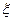 的分布列及数学期望
的分布列及数学期望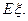
(本小题满分13分)
已知向量 且与向量
且与向量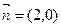 所成角为
所成角为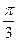 ,其中A,B,C是
,其中A,B,C是 的内角。
的内角。
(1)求角B的大小;
(2)求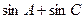 的取值范围。
的取值范围。