已知函数y=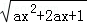 的定义域为R.
的定义域为R.
(1)求a的取值范围.
(2)若函数的最小值为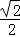 ,解关于x的不等式x2﹣x﹣a2﹣a<0.
,解关于x的不等式x2﹣x﹣a2﹣a<0.
已知△ABC的顶点A(5,1),AB边上的中线CM所在直线方程为2x﹣y﹣5=0.AC边上的高BH所在直线为x﹣2y﹣5=0.求:(1)顶点C的坐标;(2)直线BC的方程.
在△ABC中,a,b,c分别是角A,B,C的对边,且2cosAcosC+1=2sinAsinC.
(Ⅰ)求B的大小;
(Ⅱ)若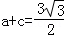 ,
,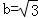 ,求△ABC的面积.
,求△ABC的面积.
设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若l在两坐标轴上的截距相等,求l的方程;
(2)若l不经过第二象限,求实数a的取值范围.
已知某几何体的俯视图是如图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S