如图，抛物线y=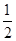
x2+mx+n与直线y=-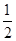x+3交于A，B两点，交x轴与D，C两点，连接AC，BC，已知A（0，3），C（3，0）．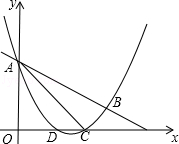
（Ⅰ）求抛物线的解析式和tan∠BAC的值；
（Ⅱ）在（Ⅰ）条件下：
（1）P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P使得以A，P，Q为顶点的三角形与△ACB相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．
（2）设E为线段AC上一点（不含端点），连接DE，一动点M从点D出发，沿线段DE以每秒一个单位速度运动到E点，再沿线段EA以每秒
个单位的速度运动到A后停止，当点E的坐标是多少时，点M在整个运动中用时最少？
如图，OA．OB是⊙O的半径且OA⊥OB，作OA的垂直平分线交⊙O于点C．D，连接CB．AB．
求证：∠ABC=2∠CBO．
三角形中有3个角、3条边共6个元素，由其中的已知元素，求出所有未知元素的过程，叫做解三角形．
已知△ABC中，AB=
，∠B=45°，BC=1+
，解△ABC．
某纪念币从2013年11月11日起开始上市，通过市场调查得知该纪念币每1枚的市场价y（单位：元）与上市时间x（单位：天）的数据如下：
| 上市时间x天 |
4 |
10 |
36 |
| 市场价y元 |
90 |
51 |
90 |
（1）根据上表数据，在某一特定时期内，可从下列函数中选取一个恰当的函数描述纪念币的市场价y与上市时间x的变化关系：
①y=ax+b（a≠0）；②y=a（x-h）2+k（ a≠0）；③y=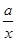
（a≠0）．
你可选择的函数的序号是 ．
（2）利用你选取的函数，求该纪念币上市多少天时市场价最低，最低价格是多少？
在一个不透明的袋子中，放入除颜色外其余都相同的1个白球、2个黑球、3个红球．搅匀后，从中随机摸出2个球．
（1）请列出所有可能的结果：
（2）求每一种不同结果的概率．
如图是汽车加油站在加油过程中，加油器仪表某一瞬间的显示，请你结合图片信息，解答下列问题：
（1）加油过程中的常量是，变量是；
（2）请用合适的方式表示加油过程中变量之间的关系．