(本小题满分12分)已知椭圆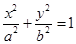
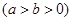 的左、右焦点分别为F1(-3,0),F2(3,0),直线y=kx与椭圆交于A、B两点.
的左、右焦点分别为F1(-3,0),F2(3,0),直线y=kx与椭圆交于A、B两点.
(Ⅰ)若三角形AF1F2的周长为 ,求椭圆的标准方程;
,求椭圆的标准方程;
(Ⅱ)若 ,且以AB为直径的圆过椭圆的右焦点,求椭圆离心率e的取值范围.
,且以AB为直径的圆过椭圆的右焦点,求椭圆离心率e的取值范围.
.已知数列 满足
满足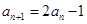 ,
, .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式和前
的通项公式和前 项和
项和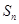 .
.
设函数
(1)求函数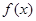 的最小正周期和单调递增区间;
的最小正周期和单调递增区间;
(2)当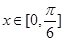 时,
时,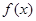 的最大值为2,求
的最大值为2,求 的值,并求出
的值,并求出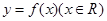 的对称
的对称
轴方程.
将一颗质地均匀的正三棱锥骰子(4个面的点数分别为1,2,3,4)先
后抛掷两次,记第一次出现的点数为 ,第二次出现的点数为
,第二次出现的点数为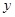
(1)求事件“ ”的概率.
”的概率.
(2)求点(x,y)落在 的区域内的概率。
的区域内的概率。
(本小题满分10分)选修4-5:不等式选讲
关于 的不等式
的不等式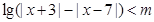 .(Ⅰ)当
.(Ⅰ)当 时,解此不等式;
时,解此不等式;
(Ⅱ)设函数 ,当
,当 为何值时,
为何值时, 恒成立?
恒成立?
(本小题满分10分)选修4-4;坐标系与参数方程
已知在平面直角坐标系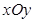 内,点
内,点 在曲线C:
在曲线C: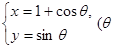 为参数
为参数 )上运动.以
)上运动.以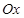 为极轴建立极坐标系,直线
为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为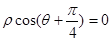
(Ⅰ)写出曲线C的标准方程和直线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)若直线 与曲线C相交于A、B两点,点M在曲线C上移动,试求
与曲线C相交于A、B两点,点M在曲线C上移动,试求 面积的最大值.
面积的最大值.