.已知数列 满足
满足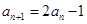 ,
, .
.
(Ⅰ)求证:数列 是等比数列;
是等比数列;
(Ⅱ)求数列 的通项公式和前
的通项公式和前 项和
项和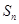 .
.
设矩阵M=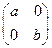 (其中a>0,b>0).
(其中a>0,b>0).
(1)若a=2,b=3,求矩阵M的逆矩阵M-1;
(2)若曲线C:x2+y2=1在矩阵M所对应的线性变换作用下得到曲线C’: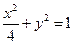 ,求a,b的值.
,求a,b的值.
设曲线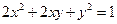 在矩阵
在矩阵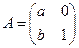 (其中a>0)对应的变换作用下得到的曲线为
(其中a>0)对应的变换作用下得到的曲线为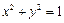 .
.
(1)求实数a,b的值.
(2)求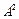 的逆矩阵.
的逆矩阵.
设不等式|x-2|<a(a∈N*)的解集为A,且 ∈A,
∈A,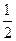 ∉A.
∉A.
(1)求a的值;
(2)求函数f(x)=|x+a|+|x-2|的最小值.
已知函数f(x)=|2x-1|+|2x+a|,g(x)=x+3.
(1)当a=-2时,求不等式f(x)<g(x)的解集;
(2)设a>-1,且当x∈[-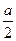 ,
, )时, f(x)≤g(x),求a的取值范围.
)时, f(x)≤g(x),求a的取值范围.
已知函数f(x)=|x-a|,其中a>1.
(1)当a=2时,求不等式f(x)≥4-|x-4|的解集;
(2)已知关于x的不等式|f(2x+a)-2f(x)|≤2的解集为{x|1≤x≤2},求a的值.