如图,分别延长平行四边形ABCD的边CD、AB到E、F,使DE=BF= CD,连接EF,分别交AD,BC于G,H,连接CG,AH
CD,连接EF,分别交AD,BC于G,H,连接CG,AH
(1)求证:四边形AGCH为平行四边形;
(2)求△DEG和△CGH的面积比.
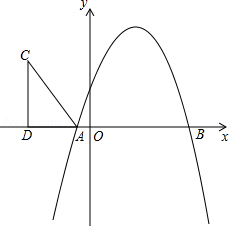
如图,抛物线 与 轴分别交于 , 两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点 ,作 垂直 轴于点 ,连接 ,且 , ,将 沿 轴向右平移 个单位,当点 落在抛物线上时,求 的值;
(3)在(2)的条件下,当点 第一次落在抛物线上记为点 ,点 是抛物线对称轴上一点.试探究:在抛物线上是否存在点 ,使以点 、 、 、 为顶点的四边形是平行四边形?若存在,请求出点 的坐标;若不存在,请说明理由.
如图, 是 的直径,点 在 的延长线上, 平分 交 于点 ,且 ,垂足为点 .
(1)求证:直线 是 的切线.
(2)若 , ,求弦 的长.

如图,一次函数 的图象与反比例函数 的图象交于点 , 两点.
(1)求一次函数与反比例函数的解析式;
(2)求 的面积.

如图,为了测量某条河的宽度,现在河边的一岸边任意取一点 ,又在河的另一岸边取两点 、 测得 , ,量得 长为100米.求河的宽度(结果保留根号).

用 、 两种机器人搬运大米, 型机器人比 型机器人每小时多搬运20袋大米, 型机器人搬运700袋大米与 型机器人搬运500袋大米所用时间相等.求 、 型机器人每小时分别搬运多少袋大米.