如图1,在平面直角坐标系中,正方形OABC的顶点A和C分别在x轴和y轴正半轴上,点B坐标为(3,3),抛物线y=﹣x2+bx+c过点A、C,交x轴负半轴于点D,与BC边的另一个交点为E,抛物线的顶点为M,对称轴交x轴于点N.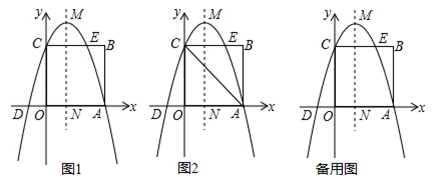
(1)求抛物线的函数关系式;
(2)点P在直线MN上,求当PE+PA的值最小时点P的坐标;
(3)如图2,探索在x轴是否存在一点F,使∠CFO=∠CDO﹣∠CAO?若存在,求点F的坐标;不存在,说明理由;
(4)将抛物线沿y轴方向平移m个单位后,顶点为Q,若QO平分∠CQN,求点Q的坐标.
一个多项式减去多项式 ,糊涂同学将减号抄成了加号,运算结果为
,糊涂同学将减号抄成了加号,运算结果为 ,求原题的正确结果。
,求原题的正确结果。
先化简,再求值:
如图,△ABC的边BC在直线l上,AD是△ABC的高,∠ABC=45°,BC=6cm,AB=2 cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题:
cm.点P从点B出发沿BC方向以1cm/s速度向点C运动,当点P到点C时,停止运动.PQ⊥BC,PQ交AB或AC于点Q,以PQ为一边向右侧作矩形PQRS,PS=2PQ.矩形PQRS与△ABC的重叠部分的面积为S(cm2),点P的运动时间为t(s).回答下列问题: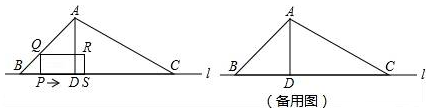
(1)AD= cm;
(2)当点R在边AC上时,求t的值;
(3)求S与t之间的函数关系式.
在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)与销售单价x(元/个)之间的对应关系如图所示:
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查的销售规律,求销售利润w(元)与销售单价x(元/个)之间的函数关系式;
(3)在(2)的条件下,若许愿瓶的进货成本不超过900元,要想获得最大利润,试确定这种许愿瓶的销售单价,并求出此时的最大利润.
如图,已知抛物线经过点A(-1,0)、B(3,0)、C(0,3)三点.
(1)求抛物线的解析式.
(2)点M是线段BC上的点(不与B,C重合),过M作MN∥y轴交抛物线于N,若点M的横坐标为m,请用m的代数式表示MN的长.
(3)在(2)的条件下,连接NB、NC,是否存在m,使△BNC的面积最大?若存在,求m的值;若不存在,说明理由.