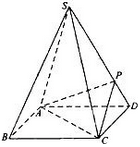
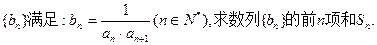(本小题满分12分)如图,正四棱锥 中,
中,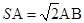 .
.
(1)求证: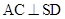 ;
;
(2)在线段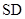 上是否存在点
上是否存在点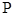 ,使得二面角
,使得二面角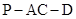 的大小为
的大小为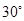 ,若存在,求出
,若存在,求出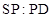 ;若不存在,试说明理由.
;若不存在,试说明理由.
(本小题满分12分)
已知函数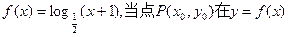 的图象上移动时,点
的图象上移动时,点 的图象上移动。
的图象上移动。
(I)点P的坐标为(1,-1),点Q也在 的图象上,求t的值;
的图象上,求t的值;
(II)求函数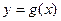 的解析式;
的解析式;
(III)若方程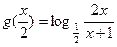 的解集是
的解集是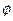 ,求实数t的取值范围。
,求实数t的取值范围。
(本小题满分12分)
已知函数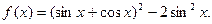
(I)若将函数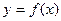 的图象向左平移
的图象向左平移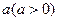 个单位长度得到的图象恰好关于点
个单位长度得到的图象恰好关于点 对称,求实数a的最小值;
对称,求实数a的最小值;
(II)若函数 上为减函数,试求实数b的值。
上为减函数,试求实数b的值。
(本小题满分13分)
已知数列 }满足:
}满足:
(I)令 为等差数列;
为等差数列;
(II)求
(本小题满分13分)
已知函数
(1)求函数 的最小正周期和图象的对称
的最小正周期和图象的对称 轴方程;
轴方程;
(2)求函数 上的值域。
上的值域。
(本不上题满分13分)
已知公差不为零的等差数列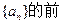 6项和为60,且
6项和为60,且 的等比中项。
的等比中项。
(1)求数列 的
的 通项公式;
通项公式;
(2)若数列