(本小题满分10分)选修4-1:几何证明选讲
如图,直线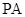 与圆相切于点
与圆相切于点 ,过
,过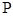 作直线与圆交于
作直线与圆交于 、
、 两点,点
两点,点 在圆上,且
在圆上,且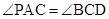 .
.
(1)证明: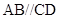 ;
;
(2)若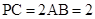 ,求
,求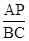 .
.
(本小题满分14分)
已知函数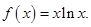
(Ⅰ)求函数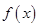 的极值点;
的极值点;
(Ⅱ)若直线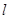 过点
过点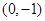 且与曲线
且与曲线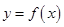 相切,求直线
相切,求直线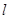 的方程;
的方程;
(Ⅲ)设函数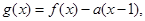
 求函数
求函数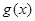 在
在 上的最小值.(
上的最小值.( 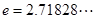 )
)
(本小题满分12分)
经市场调查,某旅游城市在过去的一个月内(以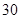 天计),第
天计),第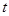 天
天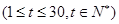 的旅游人数
的旅游人数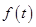 (万人)近似地满足
(万人)近似地满足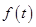 =4+
=4+ ,而人均消费
,而人均消费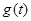 (元)近似地满足
(元)近似地满足 .
.
(Ⅰ)求该城市的旅游日收益 (万元)与时间
(万元)与时间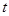
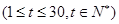 的函数关系式;
的函数关系式;
(Ⅱ)求该城市旅游日收益的最小值.
(本小题满分12分)
若二次函数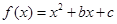 满足
满足 ,且函数的
,且函数的 的一个零点为
的一个零点为 .
.
(Ⅰ) 求函数 的解析式;
的解析式;
(Ⅱ)对任意的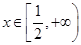 ,
, 恒成立,求实数
恒成立,求实数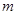 的取值范围.
的取值范围.
(本小题满分12分)
已知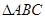 的角A、B、C所对的边分别是
的角A、B、C所对的边分别是 ,设向量
,设向量 ,
,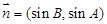 ,
, 
(Ⅰ)若 ∥
∥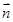 ,求证:
,求证: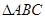 为等腰三角形;
为等腰三角形;
(Ⅱ)若 ⊥
⊥ ,边长
,边长 ,
, ,求
,求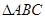 的面积.
的面积.
(本小题满分12分)
记函数 的定义域为集合
的定义域为集合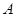 ,函数
,函数 的定义域为集合
的定义域为集合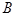 .
.
(Ⅰ)求 ;
;
(Ⅱ)若 ,且
,且 ,求实数
,求实数 的取值范围.
的取值范围.