(本小题满分14分)
已知函数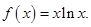
(Ⅰ)求函数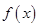 的极值点;
的极值点;
(Ⅱ)若直线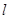 过点
过点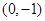 且与曲线
且与曲线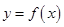 相切,求直线
相切,求直线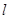 的方程;
的方程;
(Ⅲ)设函数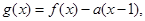
 求函数
求函数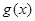 在
在 上的最小值.(
上的最小值.( 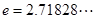 )
)
四棱锥P—ABCD中,PA⊥面ABCD,PA=AB=BC=2,E为PA中点,过E作平行于底面的面EFGH分别与另外三条侧棱交于F,G,H,已知底面ABCD为直角梯形,AD//BC,AB⊥AD,∠BCD=135°
(1)求异面直线AF,BG所成的角的大小;
(2)设面APB与面CPD所成的锐二面角的大小为θ,求cosθ.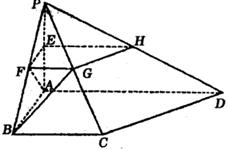
如图,已知长方体

 直线
直线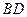 与平面
与平面 所成的角为
所成的角为 ,
, 垂直
垂直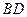 于
于 ,
, 为
为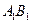 的中点.
的中点.
(1)求异面直线 与
与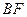 所成的角;
所成的角;
(2)求平面 与平面
与平面 所成的二面角;
所成的二面角;
(3)求点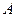 到平面
到平面 的距离.
的距离.
如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=AB=2,E,F分别是AB与PD的中点.
(1)求证:PC⊥BD;
(2)求证:AF//平面PEC;
(3)求二面角P—EC—D的大小.
如图,在边长为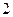 的正方形
的正方形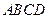 中,点
中,点 是
是 的中点,点
的中点,点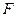 是
是 的中点,将△AED,△DCF分别沿
的中点,将△AED,△DCF分别沿 折起,使
折起,使 两点重合于
两点重合于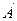 .
.
(1) 求证: ;
;
(2) 求二面角 的正切值.
的正切值.
如图,在△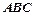 中,
中,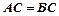 ,
, ,
, 为
为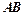 的中点,沿
的中点,沿 将△
将△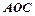 折起到△
折起到△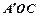 的位置,使得直线
的位置,使得直线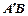 与平面
与平面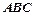 成
成 角。
角。
(1)若点 到直线
到直线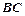 的距离为
的距离为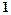 ,求二面角
,求二面角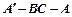 的大小;
的大小;
(2)若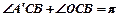 ,求
,求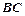 边的长。
边的长。