(本小题满分10分)选修4-5:不等式选讲
设实数 ,
, 满足
满足 .
.
(1)若 ,求
,求 的取值范围;
的取值范围;
(2)求 最小值.
最小值.
若直线mx+y+2=0与线段AB有交点,其中A(-2, 3),B(3,2),求实数m的取值范围。
给定抛物线C: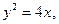 F是C的焦点,过点F的直线
F是C的焦点,过点F的直线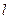 与C相交于A、B两点.
与C相交于A、B两点.
(Ⅰ)设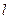 的斜率为1,求
的斜率为1,求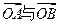 夹角的大小;
夹角的大小;
(Ⅱ)设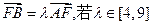 ,求
,求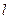 在
在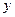 轴上截距的变化范围.
轴上截距的变化范围.
如图,在底面是菱形的四棱锥P—ABCD中,∠ABC=600,PA=AC=a,PB=PD=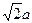 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(1)证明PA⊥平面ABCD;
(2)求以AC为棱,EAC与DAC为面的二面角 的大小;
的大小;
(3)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.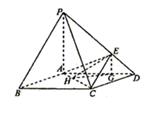
在三棱锥S—ABC中,△ABC是边长为4的正三角形,平面SAC⊥平面ABC,SA=SC=2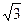 ,M、N分别为AB、SB的中点.
,M、N分别为AB、SB的中点.
(Ⅰ)证明:AC⊥SB;
(Ⅱ)求二面角N—CM—B的大小;
(Ⅲ)求点B到平面CMN的距离.
在平面几何中,我们学习了这样一个命题:过三角形的内心作一直线,将三角形分成的两部分的周长比等于其面积比。请你类比写出在立体几何中,有关四面体的相似性质,并证之。