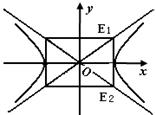
如图所示,在三棱锥S﹣ABC中,SA⊥SB,SB⊥SC,SC⊥SA,且SA,SB,SC和底面ABC所成的角分别为α1,α2,α3,△SBC,△SAC,△SAB的面积分别为S1,S2,S3,类比三角形中的正弦定理,给出空间图形的一个猜想是 .

若直角坐标平面内两点P、Q满足条件:①P、Q都在函数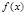 的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数
的图象上;②P、Q关于原点对称,则称点对(P,Q)是函数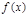 的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数
的一个“友好点对”(点对(P,Q)与(Q,P)看作同一个“友好点对”).已知函数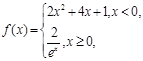 则
则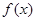 的“友好点对”有
的“友好点对”有
个.
某人午休醒来,发觉表停了,他打开收音机想收听电台整点报时,则他等待的时间短于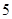 分钟的概率为.
分钟的概率为.
设函数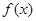 的定义域为D,若存在非零数
的定义域为D,若存在非零数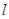 使得对于任意
使得对于任意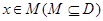 有
有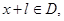 且
且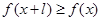 ,则称
,则称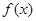 为M上的
为M上的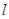 高调函数。
高调函数。
现给出下列命题:
①函数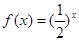 为R上的1高调函数;
为R上的1高调函数;
②函数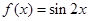 为R上的
为R上的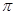 高调函数
高调函数
③如果定义域为 的函数
的函数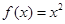 为
为 上
上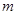 高调函数,那么实数
高调函数,那么实数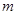 的取值范围是
的取值范围是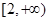
其中正确的命题是。(写出所有正确命题的序号)
设长方体的长、宽、高分别为2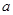 、
、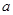 、
、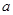 ,其顶点都在一个球面上,则该球的表面积为 _________.
,其顶点都在一个球面上,则该球的表面积为 _________.
如图所示,直线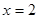 与双曲线C:
与双曲线C: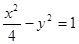 的渐近线交于
的渐近线交于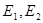 两点,记
两点,记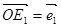 ,
,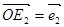 .任取双曲线C上的点
.任取双曲线C上的点 ,若
,若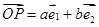 (
(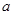 、
、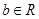 ),则
),则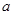 、
、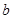 满足的一个等式是.
满足的一个等式是.