有编号为1,2,3,…,n的n个学生,入坐编号为1,2,3,…n的n个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为ξ,已知ξ=2时,共有6种坐法.
(1)求n的值;
(2)求随机变量ξ的概率分布列和数学期望.
(本小题满分12分)
已知二项式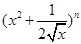 (
( N*)展开式中,前三项的二项式系数和是
N*)展开式中,前三项的二项式系数和是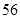 ,求:
,求:
(Ⅰ) 的值;
的值;
(Ⅱ)展开式中的常数项.
已知定义在 的函数
的函数 ,对任意的
,对任意的 、
、 ,都有
,都有 ,且当
,且当 时,
时, .
.
(1)证明:当 时,
时, ;
;
(2)判断函数 的单调性并加以证明;
的单调性并加以证明;
(3)如果对任意的 、
、 ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
设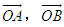 为两个不共线向量.
为两个不共线向量.
(1)试确定实数k,使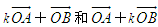 共线;
共线;
(2) ,求使
,求使 三个向量的终点在同一条直线上的
三个向量的终点在同一条直线上的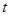 的值.
的值.
商场销售某一品牌的羊毛衫,购买人数是羊毛衫标价的一次函数,标价越高,购买人数越少.把购买人数为零时的最低标价称为无效价格,已知无效价格为每件300元.现在这种羊毛衫的成本价是100元/ 件,商场以高于成本价的价格(标价)出售. 问:
(1)商场要获取最大利润,羊毛衫的标价应定为每件多少元?
(2)通常情况下,获取最大利润只是一种“理想结果”,如果商场要获得最大利润的75%,那么羊毛衫的标价为每件多少元?
已知 ,设
,设 .
.
(1)求函数 的最小正周期,并写出
的最小正周期,并写出 的减区间;
的减区间;
(2)当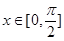 时,求函数
时,求函数 的最大值及最小值.
的最大值及最小值.