计算：-优题课

在太空种子种植体验实践活动中，为了解"宇番2号"番茄，某校科技小组随机调查60株番茄的挂果数量 $x$ （单位：个），并绘制如下不完整的统计图表：

"宇番2号"番茄挂果数量统计表

挂果数量 $x$ （个）	频数（株）	频率
$25 ⩽ x < 35$	6	0.1
$35 ⩽ x < 45$	12	0.2
$45 ⩽ x < 55$	$a$	0.25
$55 ⩽ x < 65$	18	$b$
$65 ⩽ x < 75$	9	0.15

请结合图表中的信息解答下列问题：

（1）统计表中， $a =$ 　　， $b =$ 　　；

（2）将频数分布直方图补充完整；

（3）若绘制"番茄挂果数量扇形统计图"，则挂果数量在" $35 ⩽ x < 45$ "所对应扇形的圆心角度数为　　 $°$ ；

（4）若所种植的"宇番2号"番茄有1000株，则可以估计挂果数量在" $55 ⩽ x < 65$ "范围的番茄有　　株．

世界读书日，某书店举办“书香”图书展，已知《汉语成语大词典》和《中华上下五千年》两本书的标价总和为150元，《汉语成语大词典》按标价的 $50 %$ 出售，《中华上下五千年》按标价的 $60 %$ 出售，小明花80元买了这两本书，求这两本书的标价各多少元．

计算：

（1） $6 \div (- 3) + \sqrt{4} - 8 \times 2^{- 2}$ ；

（2）解不等式组： $\{\begin{matrix} x - 1 < 2 \\ \frac{x + 1}{2} ⩾ 1 \end{matrix}$ ．

有一列按一定顺序和规律排列的数：

第一个数是 $\frac{1}{1 \times 2}$ ；

第二个数是 $\frac{1}{2 \times 3}$ ；

第三个数是 $\frac{1}{3 \times 4}$ ；

$\dots$

对任何正整数 $n$ ，第 $n$ 个数与第 $(n + 1)$ 个数的和等于 $\frac{2}{n \times (n + 2)}$ ．

（1）经过探究，我们发现： $\frac{1}{1 \times 2} = \frac{1}{1} - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ ，

设这列数的第5个数为 $a$ ，那么 $a > \frac{1}{5} - \frac{1}{6}$ ， $a = \frac{1}{5} - \frac{1}{6}$ ， $a < \frac{1}{5} - \frac{1}{6}$ ，哪个正确？

请你直接写出正确的结论；

（2）请你观察第1个数、第2个数、第3个数，猜想这列数的第 $n$ 个数（即用正整数 $n$ 表示第 $n$ 数），并且证明你的猜想满足"第 $n$ 个数与第 $(n + 1)$ 个数的和等于 $\frac{2}{n \times (n + 2)}$ "；

（3）设 $M$ 表示 $\frac{1}{1^{2}}$ ， $\frac{1}{2^{2}}$ ， $\frac{1}{3^{2}}$ ， $\dots$ ， $\frac{1}{2016^{2}}$ ，这2016个数的和，即 $M = \frac{1}{1^{2}} + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \dots \frac{1}{2016^{2}}$ ，

求证： $\frac{2016}{2017} < M < \frac{4031}{2016}$ ．

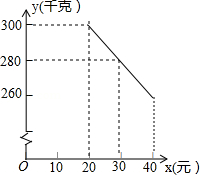
草莓是云南多地盛产的一种水果，今年某水果销售店在草莓销售旺季，试销售成本为每千克20元的草莓，规定试销期间销售单价不低于成本单价，也不高于每千克40元，经试销发现，销售量 $y$ （千克）与销售单价 $x$ （元）符合一次函数关系，如图是 $y$ 与 $x$ 的函数关系图象．

（1）求 $y$ 与 $x$ 的函数解析式（也称关系式）；

（2）设该水果销售店试销草莓获得的利润为 $W$ 元，求 $W$ 的最大值．