在Rt△ABC中，∠ACB=90°，tan∠BAC=
．点D在边AC上（不与A，C重合），连接BD，F为BD中点．
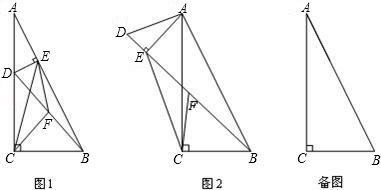
（1）若过点D作DE⊥AB于E，连接CF、EF、CE，如图1．设CF=kEF，则k= ；
（2）若将图1中的△ADE绕点A旋转，使得D、E、B三点共线，点F仍为BD中点，如图2所示．求证：BE-DE=2CF；
（3）若BC=6，点D在边AC的三等分点处，将线段AD绕点A旋转，点F始终为BD中点，求线段CF长度的最大值．
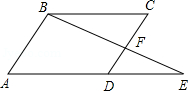
如图，AB∥EF∥CD，已知AC+BD=120，BC=50，EC+ED=96，求CF．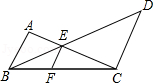
已知：∠1=∠2，CD=DE，EF∥AB，求证：EF=AC．
如图，在△ABC中，D为BC边的中点，E为AC边上的任意一点，BE交AD与点O，某学生在研究这一问题时，发现了如下事实，
①当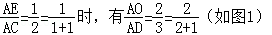
；
②当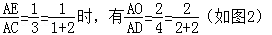
；
③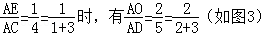
；
如图4中，当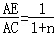
时，请你猜想
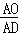的一般结论，并证明你的结论（其中n为正整数）．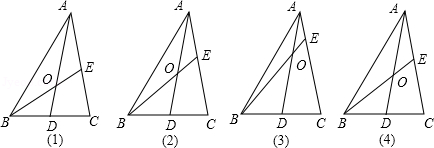
如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′=EB．类似地，在AB上折出点B″使AB″=AB′．这时B″就是AB的黄金分割点．请你证明这个结论．
如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即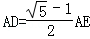
，BE交DC于点F，已知
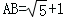，求CF的长．