阅读材料：
例：说明代数式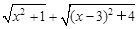 
的几何意义，并求它的最小值．
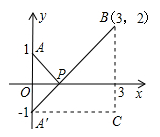
解：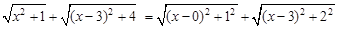
，如图，建立平面直角坐标系，点P（x，0）是x轴上一点，则
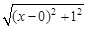可以看成点P与点A（0，1）的距离，
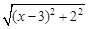可以看成点P与点B（3，2）的距离，所以原代数式的值可以看成线段PA与PB长度之和，它的最小值就是PA＋PB的最小值．
设点A关于x轴的对称点为A′，则PA＝PA′，因此，求PA＋PB的最小值，只需求PA′＋PB的最小值，而点A′、B间的直线段距离最短，所以PA′＋PB的最小值为线段A′B的长度．为此，构造直角三角形A′CB，因为A′C＝3，CB＝3，所以A′B＝
，即原式的最小值为．
根据以上阅读材料，解答下列问题：
（1）代数式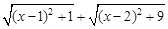
的值可以看成平面直角坐标系中点P（x，0）与点A（1，1）、点B 的距离之和．（填写点B的坐标）
（2）代数式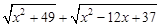 
的最小值．
（年贵州省毕节）如图，将▱ABCD的AD边延长至点E，使DE=
AD，连接CE，F是BC边的中点，连接FD．
（1）求证：四边形CEDF是平行四边形；
（2）若AB=3，AD=4，∠A=60°，求CE的长．
（年贵州省贵阳市）如图，在Rt△ABC中，∠ACB=90°，D为AB的中点，且AE∥CD，CE∥AB．
（1）四边形ADCE是菱形；
（2）若∠B=60°，BC=6，求菱形ADCE的高．（计算结果保留根号）
（年云南省）如图，在矩形ABCD中，AB=4，AD=6，M，N分别是AB，CD的中点，P是AD上的点，且∠PNB=3∠CBN．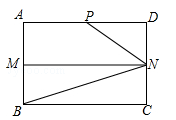
（1）求证：∠PNM=2∠CBN；
（2）求线段AP的长．
（年云南省曲靖市）如图，菱形ABCD的对角线AC与BD相交于点O，且BE∥AC，CE∥BD．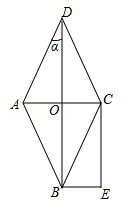
（1）求证：四边形OBEC是矩形；
（2）若菱形ABCD的周长是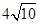
，tanα=
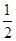，求四边形OBEC的面积．
（年贵州省黔南州）如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．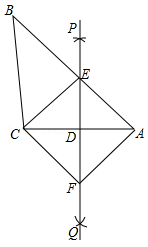
（1）求证：△AED≌△CFD；
（2）求证：四边形AECF是菱形．
（3）若AD=3，AE=5，则菱形AECF的面积是多少？