如图1是一种包装盒的表面展开图，将它围起来可得到一个几何体的-优题课

如图1是一种包装盒的表面展开图，将它围起来可得到一个几何体的模型．

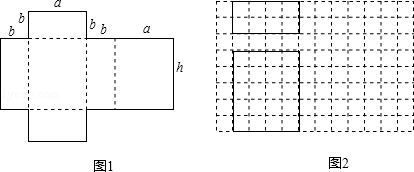
（1）这个几何体模型的名称是．
（2）如图2是根据a，b，h的取值画出的几何体的主视图和俯视图（图中实线表示的长方形），请在网格中画出该几何体的左视图．
（3）若h=a+b，且a，b满足a²+b²﹣a﹣6b+10=0，求该几何体的表面积．

科目数学题型解答题难度中等

知识点：中心投影

先化简，再求值： $1 - \frac{y - x}{x + 2 y} \div \frac{x^{2} - y^{2}}{x^{2} + 4 xy + 4 y^{2}}$ ；其中 $x = \cos 30 ° \times \sqrt{12}$ ， $y = {(π - 3)}^{0} - {(\frac{1}{3})}^{- 1}$ ．

如图，在四边形 $ABCD$ 中， $∠ A = ∠ C = 90 °$ ， $DE$ ， $BF$ 分别平分 $∠ ADC$ ， $∠ ABC$ ，并交线段 $AB$ ， $CD$ 于点 $E$ ， $F$ （点 $E$ ， $B$ 不重合）．在线段 $BF$ 上取点 $M$ ， $N$ （点 $M$ 在 $BN$ 之间），使 $BM = 2 FN$ ．当点 $P$ 从点 $D$ 匀速运动到点 $E$ 时，点 $Q$ 恰好从点 $M$ 匀速运动到点 $N$ ．记 $QN = x$ ， $PD = y$ ，已知 $y = - \frac{6}{5} x + 12$ ，当 $Q$ 为 $BF$ 中点时， $y = \frac{24}{5}$ ．

（1）判断 $DE$ 与 $BF$ 的位置关系，并说明理由．

（2）求 $DE$ ， $BF$ 的长．

（3）若 $AD = 6$ ．

①当 $DP = DF$ 时，通过计算比较 $BE$ 与 $BQ$ 的大小关系．

②连结 $PQ$ ，当 $PQ$ 所在直线经过四边形 $ABCD$ 的一个顶点时，求所有满足条件的 $x$ 的值．

某经销商3月份用18000元购进一批 $T$ 恤衫售完后，4月份用39000元购进一批相同的 $T$ 恤衫，数量是3月份的2倍，但每件进价涨了10元．

（1）4月份进了这批 $T$ 恤衫多少件？

（2）4月份，经销商将这批 $T$ 恤衫平均分给甲、乙两家分店销售，每件标价180元．甲店按标价卖出 $a$ 件以后，剩余的按标价八折全部售出；乙店同样按标价卖出 $a$ 件，然后将 $b$ 件按标价九折售出，再将剩余的按标价七折全部售出，结果利润与甲店相同．

①用含 $a$ 的代数式表示 $b$ ．

②已知乙店按标价售出的数量不超过九折售出的数量，请你求出乙店利润的最大值．

如图， $C$ ， $D$ 为 $⊙ O$ 上两点，且在直径 $AB$ 两侧，连结 $CD$ 交 $AB$ 于点 $E$ ， $G$ 是 $\hat{AC}$ 上一点， $∠ ADC = ∠ G$ ．

（1）求证： $∠ 1 = ∠ 2$ ．

（2）点 $C$ 关于 $DG$ 的对称点为 $F$ ，连结 $CF$ ．当点 $F$ 落在直径 $AB$ 上时， $CF = 10$ ， $\tan ∠ 1 = \frac{2}{5}$ ，求 $⊙ O$ 的半径．

已知抛物线 $y = a x^{2} + bx + 1$ 经过点 $(1, - 2)$ ， $(- 2, 13)$ ．

（1）求 $a$ ， $b$ 的值．

（2）若 $(5, y_{1})$ ， $(m, y_{2})$ 是抛物线上不同的两点，且 $y_{2} = 12 - y_{1}$ ，求 $m$ 的值．

试卷网试题网古诗词网作文网范文网