(本小题满分12分)已知 恒成立,
恒成立, 方程
方程 表示焦点在
表示焦点在 轴上的椭圆,若命题“
轴上的椭圆,若命题“ 且
且 ”为假,求实数
”为假,求实数 的取值范围.
的取值范围.
已知函数 在
在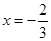 与
与 时都取得极值
时都取得极值
(1)求 的值与函数
的值与函数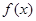 的单调区间
的单调区间
(2)若对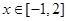 ,不等式
,不等式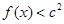 恒成立,求
恒成立,求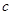 的取值范围
的取值范围
已知函数f(x)= x2+lnx.
x2+lnx.
(1)求函数f(x)的单调区间;
(2)求证:当x>1时, x2+lnx<
x2+lnx< x3.
x3.
若 展开式中第二、三、四项的二项式系数成等差数列.
展开式中第二、三、四项的二项式系数成等差数列.
(1)求n的值;
(2)此展开式中是否有常数项,为什么?
有4名男生、5名女生,全体排成一行,问下列情形各有多少种不同的排法?
(1)甲不在中间也不在两端;
(2)甲、乙两人必须排在两端;
(3)男、女生分别排在一起;
(4)男女相间;
(5)甲、乙、丙三人从左到右顺序保持一定.
已知函数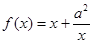 ,
,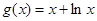 ,其中
,其中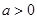 。
。
(1)若 是函数
是函数 的极值点,求实数
的极值点,求实数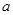 的值。
的值。
(2)若对任意的 ,
, (
(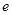 为自然对数的底数)都有
为自然对数的底数)都有 成立,求实数
成立,求实数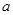 的取值范围。
的取值范围。