(本小题满分12分)如图,在三棱锥S -ABC中,△ABC是边长为2的正三角形,平面SAC⊥平面ABC,SA=SC= ,M为AB的中点.
,M为AB的中点.
(1)证明:AC⊥SB;
(2)求二面角S一CM-A的余弦值.
(本小题满分12分)已知函数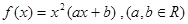 在
在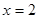 时有极值,其图象在点
时有极值,其图象在点 处的切线与直线
处的切线与直线 平行.
平行.
(1)求 的值和函数
的值和函数 的单调区间;
的单调区间;
(2)若当 时,恒有
时,恒有 ,试确定
,试确定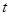 的取值范围.
的取值范围.
(本小题满分12分)设向量 ,
, ,其中
,其中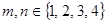 .
.
(1)请列出有序数组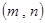 的所有可能结果;
的所有可能结果;
(2)记“使得 成立的
成立的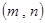 ”为事件
”为事件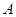 ,求事件
,求事件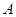 发生的概率.
发生的概率.
(本小题满分12分)如图,直三棱柱 ,底面
,底面 中,
中, ,
,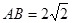 ,棱
,棱 ,
,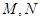 分别是
分别是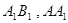 的中点.
的中点.
(1) 求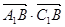 的值;
的值;
(2) 求直线 与平面
与平面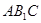 所成的角的正弦值.
所成的角的正弦值.
本题共有3个小题,第1小题满分4分,第2小题满分6分,第3小题满分8分.
(1)数列 各项均不为0,前n项和为
各项均不为0,前n项和为 ,
, ,
, 的前n项和为
的前n项和为 ,且
,且 ,若数列
,若数列 共3项,求所有满足要求的数列;
共3项,求所有满足要求的数列;
(2)求证: 是满足已知条件的一个数列;
是满足已知条件的一个数列;
(3)请构造出一个满足已知条件的无穷数列 ,并使得
,并使得 ;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
;若还能构造其他符合要求的数列,请一并写出(不超过四个)。
本题共有3个小题,第一小题3分,第二小题6分,第三小题7分
如图,曲线 由曲线
由曲线 和曲线
和曲线 组成,其中点
组成,其中点 为曲线
为曲线 所在圆锥曲线的焦点,点
所在圆锥曲线的焦点,点 为曲线
为曲线 所在圆锥曲线的焦点;
所在圆锥曲线的焦点;
(1)若 ,求曲线
,求曲线 的方程;
的方程;
(2)对于(1)中的曲线 ,若过点
,若过点 作直线
作直线 平行于曲线
平行于曲线 的渐近线,交曲线
的渐近线,交曲线 于点A、B,求三角形
于点A、B,求三角形 的面积;
的面积;
(3)如图,若直线 (不一定过
(不一定过 )平行于曲线
)平行于曲线 的渐近线,交曲线
的渐近线,交曲线 于点A、B,求证:弦AB的中点M必在曲线
于点A、B,求证:弦AB的中点M必在曲线 的另一条渐近线上。
的另一条渐近线上。