(本小题满分12分)已知椭圆C: 的离心率为
的离心率为 ,连接椭圆四个顶点形成的四边形面积为4
,连接椭圆四个顶点形成的四边形面积为4 .
.
(1)求椭圆C的标准方程;
(2)过点A(1,0)的直线与椭圆C交于点M,N,设P为椭圆上一点,且 O为坐标原点,当
O为坐标原点,当 时,求t的取值范围.
时,求t的取值范围.
已知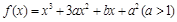 在
在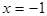 时有极值0。
时有极值0。
(1)求常数 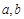 的值;
的值;
(2)求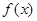 的单调区间。
的单调区间。
(3)方程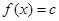 在区间[-4,0]上有三个不同的实根时实数
在区间[-4,0]上有三个不同的实根时实数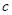 的范围。
的范围。
三个女生和五个男生排成一排.
(1)如果女生必须全排在一起,有多少种不同的排法?
(2)如果女生必须全分开,有多少种不同的排法?
(3)如果两端都不能排女生,有多少种不同的排法?
(4)如果两端不能都排女生,有多少种不同的排法?
已知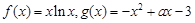 .
.
(1)求函数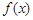 在
在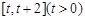 上的最小值;
上的最小值;
(2)对一切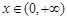 ,
,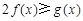 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3) 证明:对一切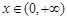 ,都有
,都有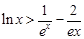 成立.
成立.
某工厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品,根据以往的经验知道,其次品率P与日产量 (件)之间近似满足关系:
(件)之间近似满足关系: (其中
(其中 为小于96的正整常数)
为小于96的正整常数)
(注:次品率P= ,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
,如P=0.1表示每生产10件产品,有1件次品,其余为合格品.)已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损A/2元,故厂方希望定出合适的日产量。
试将生产这种仪器每天的赢利T(元)表示为日产量 (件的函数);
(件的函数);
当日产量为多少时,可获得最大利润?
一个盒子装有6张卡片,上面分别写着如下6个定义域为R的函数: ,
, ,
, ,
, ,
, ,
, .
.
(1)现从盒子中任取两张卡片,将卡片上的函数相加得到一个新函数,求所得函数是奇函数的概率;
(2)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张记有偶函数的卡片则停止抽取,否则继续进行,求抽取次数ξ的分布列和数学期望.