(本小题满分12分)已知f(x)= 。
。
(1)曲线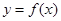 在点(1,f(1))处的切线斜率为0,求f(x)的单调区间;
在点(1,f(1))处的切线斜率为0,求f(x)的单调区间;
(2)若f(x)<x2在(1,+ )恒成立,求a的取值范围。
)恒成立,求a的取值范围。
求过两直线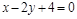 和
和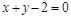 的交点, 且分别满足下列条件的直线
的交点, 且分别满足下列条件的直线 的方程
的方程
(1)直线 与直线
与直线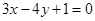 平行;
平行;
(2)直线 与直线
与直线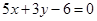 垂直.
垂直.
已知抛物线C: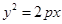
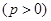 ,点A、B在抛物线C上.
,点A、B在抛物线C上.
(1)若直线AB过点M(2p,0),且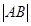 =4p,求过A,B,O(O为坐标原点)三点的圆的方程;
=4p,求过A,B,O(O为坐标原点)三点的圆的方程;
(2)设直线OA、OB的倾斜角分别为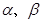 ,且
,且 ,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.
,问直线AB是否会过某一定点?若是,求出这一定点的坐标,若不是,请说明理由.
已知函数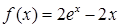 ,
,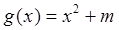 (
( ).
).
(1)试讨论函数 的单调性;
的单调性;
(2)设函数 ,
,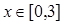 ,当函数
,当函数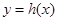 有零点时,求实数
有零点时,求实数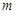 的最大值.
的最大值.
如图,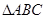 在平面
在平面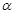 内,
内,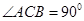 ,
, ,P为平面
,P为平面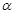 外一个动点,且PC=
外一个动点,且PC=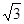 ,
,

(1)问当PA的长为多少时,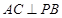
(2)当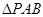 的面积取得最大值时,求直线BC与平面PAB所成角的大小
的面积取得最大值时,求直线BC与平面PAB所成角的大小
在数列{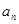 }中,
}中,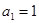 ,
,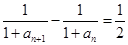
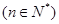 ,
,
(1)求数列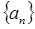 的通项公式
的通项公式
(2)设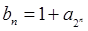 (
(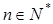 ),求数列
),求数列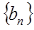 的前10项和
的前10项和 .
.