一个正方体的平面展开图及该正方体的直观图的示意图如图所示.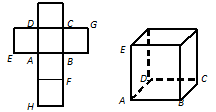
(1)请把字母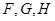 标记在正方体相应的顶点处(不需要说明理由)
标记在正方体相应的顶点处(不需要说明理由)
(2)判断平面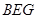 与平面
与平面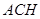 的位置关系.并证明你的结论.
的位置关系.并证明你的结论.
(3)证明:直线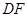
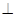 平面
平面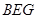
已知飞机从甲地按北偏东30°的方向飞行2000km到达乙地,再从乙地按南偏东30°的方向飞行2000km到达丙地,再从丙地按西南方向飞行1000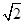 km到达丁地,问丁地在甲地的什么方向?丁地距甲地多远?
km到达丁地,问丁地在甲地的什么方向?丁地距甲地多远?
如图所示,已知▱ABCD,▱AOBE,▱ACFB,▱ACGD,▱ACDH,点O是▱ABCD的对角线交点,且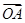 =a,
=a,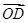 =b,
=b,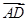 =c.
=c.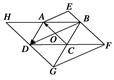
(1)写出图中与a相等的向量;
(2)写出图中与b相等的向量;
(3)写出图中与c相等的向量.
如图所示,4×3的矩形(每个小方格都是单位正方形),在起点和终点都在小方格的顶点处的向量中,试问: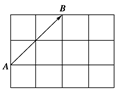
(1)与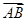 相等的向量共有几个;
相等的向量共有几个;
(2)与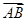 平行且模为
平行且模为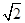 的向量共有几个?
的向量共有几个?
(3)与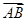 方向相同且模为3
方向相同且模为3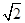 的向量共有几个?
的向量共有几个?
[分析] 非零向量平行(共线)包括两种情况:一种是方向相同,另一种是方向相反.
如图所示,四边形ABCD中,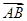 =
=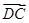 ,N、M是AD、BC上的点,且
,N、M是AD、BC上的点,且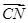 =
= .
.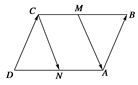
求证: =
=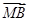 .
.
如图所示,点O为正方形ABCD对角线的交点,四边形OAED,OCFB都是正方形.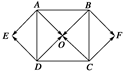
在图中所示的向量中:
(1)分别写出与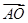 ,
,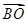 相等的向量;
相等的向量;
(2)写出与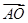 共线的向量;
共线的向量;
(3)写出与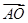 的模相等的向量;
的模相等的向量;
(4)向量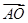 与
与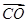 是否相等?
是否相等?