(本小题满分12分)已知椭圆C:  的离心率为
的离心率为 ,且过点(1,
,且过点(1, ).
).
(1)求椭圆C的方程;
(2)设与圆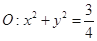 相切的直线
相切的直线 交椭圆C与A,B两点,求
交椭圆C与A,B两点,求 面积的最大值,及取得最大值时直线
面积的最大值,及取得最大值时直线 的方程.
的方程.
选修4-5:不等式选讲
设函数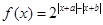 .
.
(1)当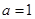 ,
,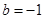 时,求使
时,求使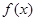 ≥
≥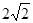 的
的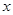 取值范围;
取值范围;
(2)若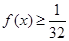 恒成立,求
恒成立,求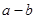 的取值范围.
的取值范围.
已知曲线C的极坐标方程是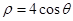 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: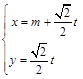 (
(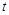 是参数).
是参数).
(1)若直线l与曲线C相交于A、B两点,且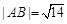 ,试求实数m值.
,试求实数m值.
(2)设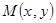 为曲线
为曲线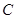 上任意一点,求
上任意一点,求 的取值范围.
的取值范围.
如图,AB是⊙O的直径,C、F是⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D.连接CF交AB于点E.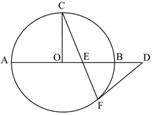
(1)求证:DE2=DB•DA;
(2)若DB=2,DF=4,试求CE的长.
已知函数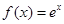 ,
,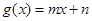 .
.
(1)设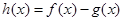 .
.
①若函数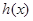 在
在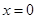 处的切线过点
处的切线过点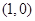 ,求
,求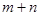 的值;
的值;
②当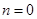 时,若函数
时,若函数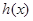 在
在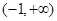 上没有零点,求
上没有零点,求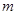 的取值范围;
的取值范围;
(2)设函数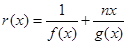 ,且
,且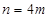 (
(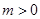 ),求证:当
),求证:当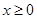 时,
时,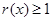 .
.
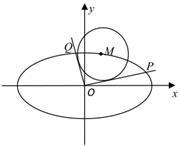
如图,已知 是椭圆
是椭圆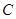 :
: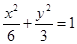 上的任一点,从原点
上的任一点,从原点 向圆
向圆 :
: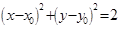 作两条切线,分别交椭圆于点
作两条切线,分别交椭圆于点 、
、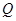 .
.
(1)若直线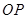 ,
,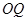 的斜率存在,并记为
的斜率存在,并记为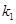 ,
,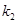 ,求证:
,求证: 为定值;
为定值;
(2)试问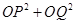 是否为定值?若是,求出该值;若不是,说明理由.
是否为定值?若是,求出该值;若不是,说明理由.