(本小题满分12分)已知直线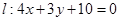 ,半径为
,半径为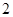 的圆
的圆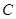 与
与 相切,圆心
相切,圆心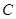 在
在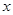 轴上且在直线
轴上且在直线 的上方
的上方
(1)求圆 的方程;
的方程;
(2)过点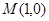 的直线与圆
的直线与圆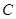 交于
交于 两点(
两点(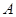 在
在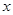 轴上方),问在
轴上方),问在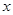 轴正半轴上是否存在点
轴正半轴上是否存在点 ,使得
,使得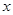 轴平分
轴平分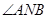 ?若存在,请求出点
?若存在,请求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
在等差数列 中,
中,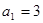 ,其前
,其前 项和为
项和为 ,等比数列
,等比数列 的各项均为正数,
的各项均为正数, ,公比为
,公比为 ,且
,且 ,
, 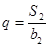 .
.
(Ⅰ)求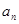 与
与 ;
;
(Ⅱ)证明: .
.
(本小题满分10分)
(1)解不等式
(2)设x,y,z 且
且 ,求
,求 的最小值.
的最小值.
本小题满分10分)
已知直线l经过点P( ,1),倾斜角
,1),倾斜角 ,在极坐标系下,圆C的极坐标方程为
,在极坐标系下,圆C的极坐标方程为 。
。
(1)写出直线l的参数方程,并把圆C的方程化为直角坐标方程;
(2)设l与圆C相交于A,B两点,求点P到A,B两点的距离之积。
(本小题满分10分)
如图,四边形ACBD内接于圆O,对角线AC与BD相交于M, AC⊥BD,E是DC中点连结EM交AB于F,作OH⊥AB于H,
求证:(1)EF⊥AB(2)OH=ME
(本小题满分12分)设函数
(1)若 ;
;
(2)若