(本小题满分12分)设函数
(1)若 ;
;
(2)若
已知函数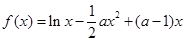 (
( 且
且 ).
).
(1)求函数 的单调区间;
的单调区间;
(2)记函数 的图象为曲线
的图象为曲线 .设点
.设点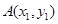 ,
, 是曲线
是曲线 上的不同两点.如果在曲线
上的不同两点.如果在曲线 上存在点
上存在点 ,使得:①
,使得:① ;②曲线
;②曲线 在点
在点 处的切线平行于直线
处的切线平行于直线 ,则称函数
,则称函数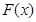 存在“中值相依切线”. 试问:函数
存在“中值相依切线”. 试问:函数 是否存在“中值相依切线”,请说明理由.
是否存在“中值相依切线”,请说明理由.
已知椭圆C: (a>b>0)的离心率为
(a>b>0)的离心率为 ,且经过点P(1,
,且经过点P(1, )。
)。
(1)求椭圆C的方程;
(2)设F是椭圆C的右焦点,M为椭圆上一点,以M为圆心,MF为半径作圆M。问点M满足什么条件时,圆M与y轴有两个交点?
(3)设圆M与y轴交于D、E两点,求点D、E距离的最大值。
已知单调递增的等比数列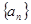 满足:
满足: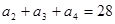 ,且
,且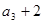 是
是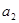 和
和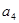 的等差中项.
的等差中项.
(1) 求数列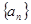 的通项公式
的通项公式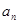 ;
;
(2) 令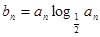 ,
,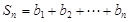 ,求使
,求使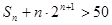 成立的最小的正整数
成立的最小的正整数 .
.
如图,多面体ABCDS中,面ABCD为矩形,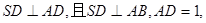
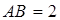 ,
,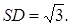
(1)求证:CD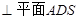 ;
;
(2)求二面角A—SB—D的余弦值.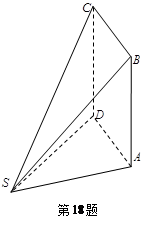
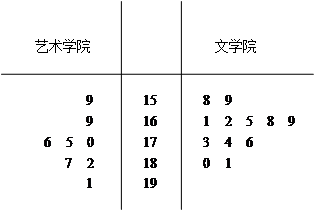
为把中国武汉大学办成开放式大学,今年樱花节武汉大学在其属下的艺术学院和文学院分别招募8名和12名志愿者从事兼职导游工作,将这20志愿者的身高编成如下茎叶图(单位:厘米)若身高在175cm及其以上定义为“高个子”,否则定义为“非高个子”且只有文学院的“高个子”才能担任兼职导游。
(1)根据志愿者的身高茎叶图指出文学院志愿者身高的中位数
(2)如果用分层抽样的方法从“高个子”和“非高个子”中抽取5人,再从这5人中选2人,那么至少有一人是“高个子”的概率是多少
(3)若从所有“高个子”中选3名志愿者。用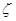 表示所选志愿者中能担任“兼职导游”的人数,试写出
表示所选志愿者中能担任“兼职导游”的人数,试写出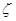 的分布列,并求
的分布列,并求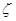 的数学期望
的数学期望