(本小题满分12分)设x1,x2是关于x的一元二次方程x2-2(m-1)x+m+5=0的两个实根,又y=x21+x22,求y=f(m)的解析式及此函数的定义域.
如图,平面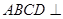 平面
平面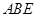 ,四边形
,四边形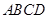 是边长为2的正方形,
是边长为2的正方形,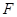 为
为 上的点,且
上的点,且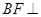 平面
平面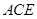 .
.
(1)求证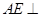 平面
平面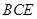 ;
;
(2)设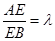 ,是否存在
,是否存在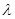 ,使二面角
,使二面角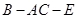 的余弦值为
的余弦值为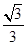 ?若存在,求
?若存在,求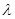 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知函数 ,其中
,其中 ,
, .若函数
.若函数 相邻两对称轴的距离等于
相邻两对称轴的距离等于 .
.
(1)求 的值;并求函数
的值;并求函数 在区间
在区间 的值域;
的值域;
(2)在△ 中,
中, 、
、 、
、 分别是角
分别是角 、
、 、
、 的对边,若
的对边,若
 ,求边
,求边 、
、 的长.
的长.
已知等差数列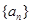 的公差
的公差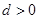 ,其前
,其前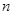 项和为
项和为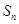 ,若
,若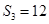 ,且
,且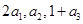 成等比数列.
成等比数列.
(1)求数列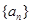 的通项公式;
的通项公式;
(2)记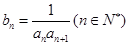 ,且数列
,且数列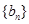 的前
的前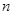 项和为
项和为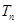 ,证明:
,证明: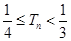 .
.
已知函数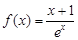 .
.
(1)求函数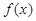 的极大值;
的极大值;
(2)设定义在 上的函数
上的函数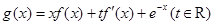 的最大值为
的最大值为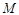 ,最小值为
,最小值为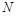 ,且
,且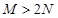 ,求实数
,求实数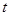 的取值范围.
的取值范围.
已知圆 ,点
,点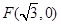 ,
, 是圆
是圆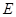 上任意一点.线段
上任意一点.线段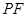 的垂直平分线和半径
的垂直平分线和半径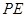 相交于
相交于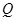 .
.
(1)求动点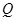 的轨迹
的轨迹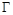 的方程;
的方程;
(2)设直线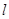 与(1)中轨迹
与(1)中轨迹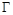 相交于
相交于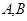 两点,直线
两点,直线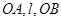 的斜率分别为
的斜率分别为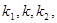
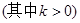 .△
.△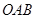 的面积为
的面积为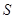 ,以
,以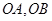 为直径的圆的面积分别为
为直径的圆的面积分别为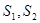 .若
.若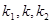 恰好构成等比数列,求
恰好构成等比数列,求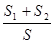 的取值范围.
的取值范围.