某高校在2012年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下图所示．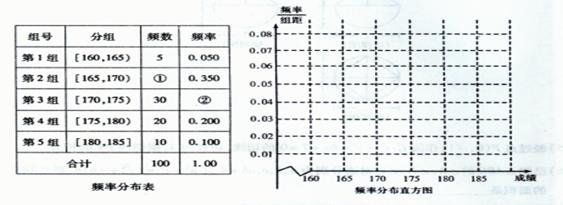
（Ⅰ）请先求出频率分布表中①、②位置相应数据，再在答题纸上完成下列频率分布直方图；
（Ⅱ）为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3、4、5组中用分层抽样抽取6名学生进入第二轮面试，求第3、4、5组每组各抽取多少名学生进入第二轮面试？
（Ⅲ）在（2）的前提下，学校决定在6名学生中随机抽取2名学生接受A考官的面试，求：第4组至少有一名学生被考官A面试的概率？
设A、B是双曲线x2-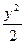
=1的上两点，点N（1，2）是线段AB的中点.（1）求直线AB的方程；（2）如果线段AB的垂直平分线与双曲线相交于C、D两点，那么A、B、C、D四点是否共圆？为什么？
过双曲线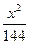
-
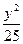=1的一个焦点作x轴的垂线，求垂线与双曲线的交点到两焦点的距离.
求与双曲线16x2-9y2=-144有共同焦点,且过点(0,2)的双曲线的方程.
给定双曲线x2-
=1,过B(1,1)能否作直线m,使m与所给双曲线交于Q1、Q2,且B为线段Q1Q2的中点?这样的直线m如果存在,求出它的方程;如果不存在,请说明理由.
设双曲线H: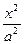 
-
=1(a>0,b>0)满足如下条件:①ab=
;②直线l过右焦点F,斜率为
,交y轴于点P,线段PF交H于Q,且|PQ|∶|QF|=2∶1.求双曲线的方程.