(本小题满分12分)已知曲线 在点
在点 处的切线的斜率为1.
处的切线的斜率为1.
(1)若函数f(x)的图象在 上为减函数,求
上为减函数,求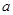 的取值范围;
的取值范围;
(2)当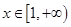 时,不等式
时,不等式 恒成立,求a的取值范围.
恒成立,求a的取值范围.
已知函数 .
(1)求曲线 在点 处的切线方程;
(2)求函数 在区间 上的最大值和最小值.
已知抛物线 过点 .过点 作直线l与抛物线C交于不同的两点M,N,过点M作x轴的垂线分别与直线OP、ON交于点A,B,其中O为原点.
(1)求抛物线C的方程,并求其焦点坐标和准线方程;
(2)求证:A为线段BM的中点.
为了研究一种新药的疗效,选100名患者随机分成两组,每组各 名,一组服药,另一组不服药.一段时间后,记录了两组患者的生理指标 和 的数据,并制成如图,其中“*”表示服药者,“+”表示未服药者.

(1)从服药的50名患者中随机选出一人,求此人指标 的值小于 的概率;
(2)从图中A,B,C,D四人中随机选出两人,记 为选出的两人中指标x的值大于1.7的人数,求 的分布列和数学期望 ;
(3)试判断这100名患者中服药者指标 数据的方差与未服药者指标y数据的方差的大小.(只需写出结论)
如图,在四棱锥 中,底面 为正方形,平面 平面 ,点M在线段PB上, 平面 , , .

(1)求证:M为PB的中点;
(2)求二面角 的大小;
(3)求直线MC与平面BDP所成角的正弦值.
在 中, , .
(1)求 的值;
(2)若 ,求 的面积.