(本小题满分12分)正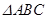 的边长为4,
的边长为4, 是
是 边上的高,
边上的高, 、
、 分别是
分别是 和
和 边的中点,现将
边的中点,现将 沿
沿 翻折成直二面角
翻折成直二面角 .
.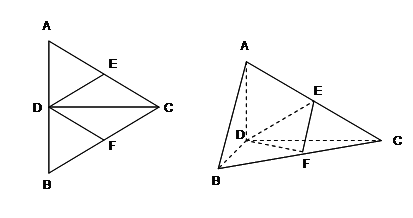
(Ⅰ)试判断直线 与平面
与平面 的位置关系,并说明理由;
的位置关系,并说明理由;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)在线段 上是否存在一点
上是否存在一点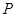 ,使
,使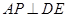 ?证明你的结论.
?证明你的结论.
已知集合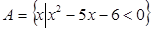 ,集合
,集合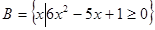 ,集合
,集合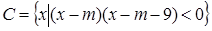
(1)求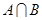 ;
;
(2)若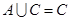 ,求实数
,求实数 的取值范围;
的取值范围;
对于函数 与常数
与常数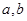 ,若
,若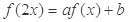 恒成立,则称
恒成立,则称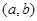 为函数
为函数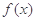 的一
的一
个“P数对”:设函数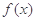 的定义域为
的定义域为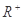 ,且
,且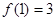 .
.
(1)若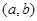 是
是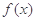 的一个“P数对”,且
的一个“P数对”,且 ,
,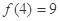 ,求常数
,求常数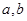 的值;
的值;
(2)若(1,1)是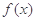 的一个“P数对”,求
的一个“P数对”,求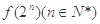 ;
;
(3)若( )是
)是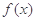 的一个“P数对”,且当
的一个“P数对”,且当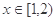 时,
时,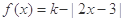 ,求k的值及
,求k的值及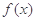 区间
区间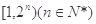 上的最大值与最小值.
上的最大值与最小值.
已知圆C: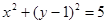 ,直线l:
,直线l: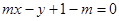 .
.
(1)求证:对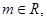 直线l与圆C总有两个不同交点;
直线l与圆C总有两个不同交点;
(2)设l与圆C交于不同两点A、B,求弦AB的中点M的轨迹方程;
(3)若定点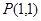 分弦
分弦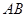 所得向量满足
所得向量满足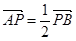 ,求此时直线l的方程.
,求此时直线l的方程.
已知E是矩形ABCD(如图1)边CD上的一点,现沿AE将△DAE折起至△D1AE(如图2),并且平面D1AE⊥平面ABCE,图3为四棱锥D1—ABCE的主视图与左视图.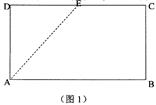
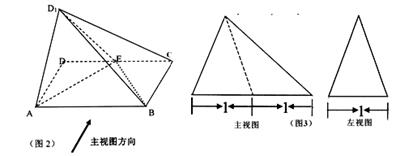
(1)求证:直线BE⊥平面D1AE;
(2)求点A到平面D1BC的距离.
设等差数列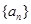 的前
的前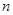 项和为
项和为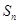 ,且
,且 ,
,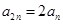 ,
,
(1)求等差数列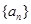 的通项公式
的通项公式 .
.
(2)令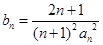 ,数列
,数列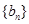 的前
的前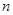 项和为
项和为 .证明:对任意
.证明:对任意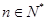 ,都有
,都有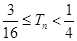 .
.