已知x,y,z均为正数,求证: +
+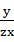 +
+ ≥
≥ +
+ +
+ .
.
已知{an}为递增的等比数列,且{a1,a3,a5}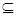 {-10,-6,-2,0,1,3,4,16}.
{-10,-6,-2,0,1,3,4,16}.
(1)求数列{an}的通项公式;
(2)是否存在等差数列{bn},使得a1bn+a2bn-1+a3bn-2+…+anb1=2n+1-n-2对一切n∈N*都成立?若存在,求出bn;若不存在,说明理由.
如图,在四棱锥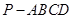 中,
中,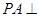 平面
平面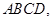 四边形
四边形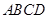 为正方形,
为正方形,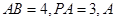 点在
点在 上的射影为
上的射影为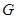 点.
点.
(1)求证: 平面
平面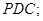
(2)在棱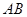 上是否存在一点
上是否存在一点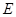 ,使得
,使得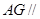 平面
平面 .若存在,求出
.若存在,求出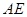 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
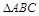 中,角A、B、C对边分别是a、b、c,满足
中,角A、B、C对边分别是a、b、c,满足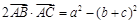 .
.
(1)求角A的大小;
(2)求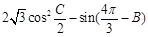 的最大值,并求取得最大值时角B、C的大小.
的最大值,并求取得最大值时角B、C的大小.
某培训班共有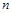 名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在
名学生,现将一次某学科考试成绩(单位:分)绘制成频率分布直方图,如图所示.其中落在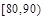 内的频数为36.
内的频数为36.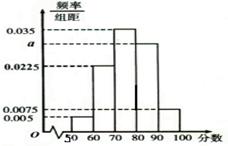
(1)请根据图中所给数据,求出a及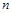 的值;
的值;
(2)从如图5组中按分层抽样的方法选取40名学生的成绩作为一个样本,求在第一组、第五组(从左到右)中分别抽取了几名学生的成绩?
(3)在(2)抽取的样本中的第一与第五组中,随机抽取两名学生的成绩,求所取两名学生的平均分不低于70分的概率.
已知 是公差为
是公差为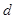 的等差数列,
的等差数列, 是公比为
是公比为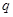 的等比数列.
的等比数列.
(Ⅰ)若 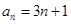 ,是否存在
,是否存在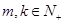 ,有
,有 ?请说明理由;
?请说明理由;
(Ⅱ)若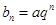 (
( 为常数,且
为常数,且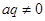 ),对任意
),对任意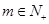 ,存在
,存在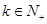 ,有
,有 ,试求
,试求 满足的充要条件;
满足的充要条件;
(Ⅲ)若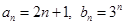 ,试确定所有的
,试确定所有的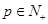 ,使数列
,使数列 中存在某个连续
中存在某个连续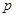 项的和为数列中
项的和为数列中 的某一项,请证明.
的某一项,请证明.