2014年6月，某中学以“我最喜爱的书籍”为主题，对学生最喜爱的一种书籍类型进行随机抽样调查，收集整理数据后，绘制出以下两幅未完成的统计图，请根据图①和图②提供的信息，解答下列问题：
（1）在这次抽样调查中，一共调查了多少名学生？
（2）请把折线统计图（图①）补充完整；
（3）如果这所中学共有学生1800名，那么请你估计最喜爱科普类书箱的学生人数．
如图，在半径为6cm的⊙O中，圆心O到弦AB的距离OE为3cm．
（1）求弦AB的长；（2）求劣弧
的长．
如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，点A，B，C的坐标分别为（0，1），（1，－1），（5，1）．
（1）直接写出点B关于原点的对称点D的坐标；
（2）将△ABC绕点C顺时针旋转90º得到△A1B1C．请在网格中画出△A1B1C，并直接写出点A1和B1的坐标．
如图，正比例函数y=2x与反比例函数
的图象的一个交点为A（2，m）．
求m和k的值．
如图，点D是△ABC的边AC上的一点，AB2＝AC·AD．求证：△ADB∽△ABC．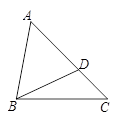
如图，在平面直角坐标系xOy中，已知点B的坐标为（2，0），点C的坐标为（0，8），sin∠CAB=
, E是线段AB上的一个动点（与点A、点B不重合），过点E作EF∥AC交BC于点F，连结CE.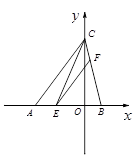
（1）求AC和OA的长；
（2）设AE的长为m，△CEF的面积为S，求S与m之间的函数关系式；
（3）在（2）的条件下试说明S是否存在最大值，若存在，请求出S的最大值，并求出此 时点E的坐标，判断此时△BCE的形状；若不存在，请说明理由．