(1)操作发现:
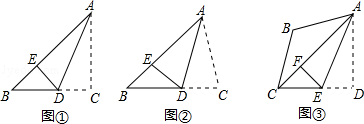
如图①,在Rt△ABC中,∠C=2∠B=90°,点D是BC上一点,沿AD折叠△ADC,使得点C恰好落在AB上的点E处.请写出AB、AC、CD之间的关系 ;
(2)问题解决:
如图②,若(1)中∠C≠90°,其他条件不变,请猜想AB、AC、CD之间的关系,并证明你的结论;
(3)类比探究:
如图③,在四边形ABCD中,∠B=120°,∠D=90°,AB=BC,AD=DC,连接AC,点E是CD上一点,沿AE折叠,使得点D正好落在AC上的F处,若BC=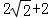 ,直接写出DE的长.
,直接写出DE的长.
我市某工艺品厂生产一款工艺品.已知这款工艺品的生产成本为每件60元.经市场调研发现:该款工艺品每天的销售量y(件)与售价x(元)之间存在着如下表所示的一次函数关系.
| 售价x(元) |
… |
70 |
90 |
… |
| 销售量y(件) |
… |
3000 |
1000 |
… |
(利润=(售价-成本价)×销售量)
(1)求销售量y(件)与售价x(元)之间的函数关系式;
(2)你认为如何定价才能使工艺品厂每天获得的利润为40 000 元?
如图,正方形网格中的每一个小正方形的边长都是1,四边形ABCD的四个顶点都在格点上,O为AD边的中点,若把四边形ABCD绕着点O顺时针旋转 ,试解决下列问题:
,试解决下列问题:
(1)画出四边形ABCD旋转后的图形;
(2)求点C旋转过程事所经过的路径长;
(3)设点B旋转后的对应点为B’,求tan∠DAB’的值.
在一次数学测验中,甲、乙两校各有100名同学参加测试.测试结果显示,甲校男生的优分率为60%,女生的优分率为40%,全校的优分率为49.6%;乙校男生的优分率为57%,女生的优分率为37%.
(男(女)生优分率=×100%,全校优分率=×100%)
(1)求甲校参加测试的男、女生人数各是多少?
(2)从已知数据中不难发现甲校男、女生的优分率都相应高于乙校男、女生的优分率,但最终的统计结果却显示甲校的全校优分率比乙校的全校的优分率低,请举例说明原因
已知反比例函数y=的图象与二次函数y=ax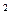 +x-1的图象相交于点(2,2)
+x-1的图象相交于点(2,2)
(1)求a和k的值;
(2)反比例函数的图象是否经过二次函数图象的顶点,为什么?
从甲地到乙地有A1、A2两条路线,从乙地到丙地有B1、B2、B3三条路线,从丙地到丁地有C1、C2两条路线.一个人任意先了一条从甲地到丁地的路线.求他恰好选到B2路线的概率是多少?