如图，有A、B两个转盘，其中转盘A被分成4等份，转盘B被分成3等份，并在每一份内标上数字，现甲、乙两人同时各转动其中一个转盘，转盘停止后（当指针指在边界线上时视为无效，重转），若将A转盘指针指向的数字记为x，B转盘指针指向的数字记为y，从而确定点P的坐标为P（x，y）．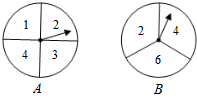
（1）请用列表或画树状图的方法写出所有可能得到的点P的坐标；
（2）李刚为甲、乙两人设计了一个游戏：记s=x+y．当s＜6时，甲获胜，否则乙获胜．你认为这个游戏公平吗？对谁有利？
（3）请你利用两个转盘，设计一个公平的游戏规则．
规定 ※ 表示一种运算，且
，求下列各式的值：
；
.
先化简，再求值：
已知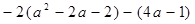 
，其中 
.
在数轴上分别表示下列各数，并比较它们的大小，用“＜”连接.
-2， -0.5，
，
， 
.
如图，在平面直角坐标系中，矩形ABCO的OA边在
轴上，OC边在
轴上，且B点坐标为（4，3）．动点M、N分别从点O、B同时出发，以1单位/秒的速度运动（点M沿OA向终点A运动，点N沿BC向终点C运动），过点N作NP∥AB交AC于点P，连结MP．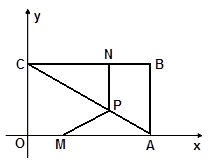
（1）直接写出OA、AB的长度；
（2）试说明△CPN∽△CAB；
（3）在两点的运动过程中，请求出ΔMPA的面积S与运动时间
的函数关系式；
（4）在运动过程中，△MPA的面积S是否存在最大值？若存在，请求出当为何值时有最大值，并求出最大值；若不存在，请说明理由．
已知：关于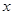
的方程
．
（1）若方程有两个相等的实数根，求
的值，并求出这时的根．
（2）问：是否存在正数，使方程的两个实数根的平方和等于136；若存在，请求出满足条件的值；若不存在，请说明理由．