某省两相近重要城市之间人员交流频繁,为了缓解交通压力,特修一条专用铁路,用一列火车作为交通车,已知该车每次拖4节车厢,一天能往返16次,如果每次拖7节车厢,则每天能往返10次.(注明:往、返各算一次)
(1)若每天往返的次数是车头每次拖挂车厢节数的一次函数,求此一次函数解析式;
(2)在(1)的条件下,每节车厢能载乘客110人,问这列火车每天往返多少次才能使运营人数最多?并求出每天最多运营人数.
如图所示,在正方体ABCDA1B1C1D1中,E、F、G、H分别是BC、CC1、C1D1、A1A的中点.求证:
(1)BF∥HD1;
(2)EG∥平面BB1D1D.
如图所示,在三棱柱ABCA1B1C1中,M、N分别是BC和A1B1的中点.求证:MN∥平面AA1C1.
如图,在三棱柱ABC-A1B1C1中,D是BC的中点.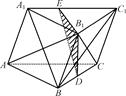
(1)若E为A1C1的中点,求证:DE∥平面ABB1A1;
(2)若E为A1C1上一点,且A1B∥平面B1DE,求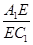 的值..
的值..
正三棱柱ABCA1B1C1中,已知AB=A1A,D为C1C的中点,O为A1B与AB1的交点.
(1)求证:AB1⊥平面A1BD;
(2)若点E为AO的中点,求证:EC∥平面A1BD.
如图所示,在直三棱柱ABCA1B1C1中,D、E分别为AA1、CC1的中点,AC⊥BE,点F在线段AB上,且AB=4AF.若M为线段BE上一点,试确定M在线段BE上的位置,使得C1D∥平面B1FM.