设函数 .
.
(1)若函数 在
在 时取得极小值,求
时取得极小值,求 的值;
的值;
(2)若函数 在定义域上是单调函数,求
在定义域上是单调函数,求 的取值范围.
的取值范围.
(本小题13分)如图1,在三棱锥P—ABC中, 平面ABC,
平面ABC, ,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。
,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示。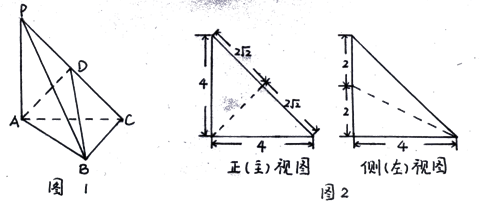
(1)证明: 平面PBC;
平面PBC;
(2)求三棱锥D—ABC的体积;
(3)在 的平分线上确定一点Q,使得
的平分线上确定一点Q,使得 平面ABD,并求此时PQ的长。
平面ABD,并求此时PQ的长。
(本小题13分)已知关于x的一元二次函数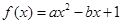 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列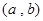 。
。
(1)若 ,
,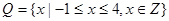 ,列举出所有的数对
,列举出所有的数对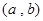 ,并求函数
,并求函数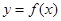 有零点的概率;
有零点的概率;
(2)若 ,
,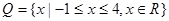 ,求函数
,求函数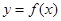 在区间
在区间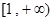 上是增函数的概率。
上是增函数的概率。
(本小题12分)一企业生产的某产品在不做电视广告的前提下,每天销售量为b件,经市场调查后得到如下规律:若对产品进行电视广告的宣传,每天的销售量S(件)与电视广告的播放量n(次)的关系可用如图所示的程序框图来体现。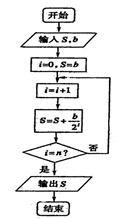

(1)试写出该产品每天的销售量S(件)关于电视广告的播放量n(次)
的函数关系式;
(2)要使该产品每天的销售量比不做电视广告时的销售量至少增加90﹪,则每天电视广告的播放量至少需要多少次?
(本小题12分)本某中学为研究学生的身体素质与课外体育锻炼时间的关系,对400名高一学生的一周课外体育锻炼时间进行调查,结果如下表所示:
| 锻炼时间(分钟) |
 |
 |
 |
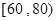 |
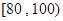 |
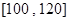 |
| 人数 |
40 |
60 |
80 |
100 |
80 |
40 |
(1)完成频率分布直方图,并估计该中学高一学生每周参加
课外体育锻炼时间的平均值(同一组中的数据用该区间的组中值作代表);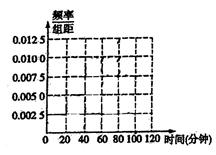
(2)现采用分层抽样的方法抽取容量为20的样本,
①应抽取多少名课外体育锻炼时间为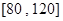 分钟的学生;
分钟的学生;
②若从①中被抽取的学生中随机抽取2名,求这2名学生课外体育锻炼时间均为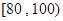 分钟的概率。
分钟的概率。
(本小题满分14分)已知在单位圆x²+y²=1上任取一点M,作MN⊥x轴,垂足为N, 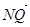 = 2
= 2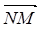 .
.
(Ⅰ)求动点Q的轨迹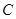 的方程;
的方程;
(Ⅱ)设点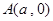 ,点
,点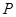 为曲线
为曲线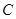 上任一点,求点
上任一点,求点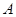 到点
到点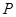 距离的最大值
距离的最大值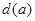 ;
;
(Ⅲ)在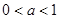 的条件下,设△
的条件下,设△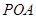 的面积为
的面积为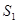 (
(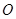 是坐标原点,
是坐标原点,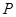 是曲线
是曲线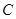 上横坐标为
上横坐标为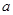 的点),以
的点),以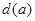 为边长的正方形的面积为
为边长的正方形的面积为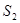 .若正数
.若正数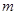 满足
满足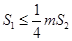 ,问
,问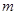 是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.
是否存在最小值,若存在,请求出此最小值,若不存在,请说明理由.