某商品进货单价为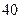 元,若销售价为
元,若销售价为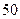 元,可卖出
元,可卖出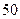 个,如果销售单价每涨
个,如果销售单价每涨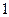 元,销售量就减少
元,销售量就减少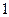 个,为了获得最大利润,则此商品的最佳售价应为多少?
个,为了获得最大利润,则此商品的最佳售价应为多少?

已知数列 的前
的前 项和为
项和为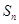 ,且
,且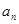 是
是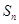 和
和 的等差中项,等差数列
的等差中项,等差数列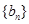 满足
满足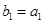 ,
,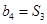 .
.
(1)求数列 、
、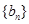 的通项公式;
的通项公式;
(2)设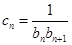 ,数列
,数列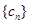 的前
的前 项和为
项和为 ,求
,求 的取值范围.
的取值范围.
已知函数f(x)=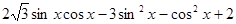 .
.
(1)当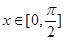 时,求
时,求 的值域;
的值域;
(2)若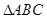 的内角
的内角 的对边分别为
的对边分别为 ,且满足
,且满足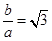 ,
,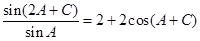 ,求
,求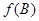 的值.
的值.
已知数列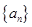 的前
的前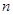 项和
项和 ,函数
,函数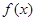 对
对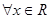 有
有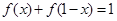 ,数列
,数列 满足
满足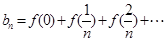
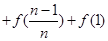 .
.
(1)分别求数列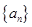 、
、 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
,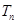 是数列
是数列 的前
的前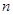 项和,若存在正实数
项和,若存在正实数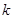 ,使不等式
,使不等式 对于一切的
对于一切的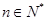 恒成立,求
恒成立,求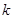 的取值范围.
的取值范围.
已知动圆过定点P(1,0),且与定直线l:x=-1相切,点C在l上.
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且斜率为-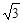 的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
的直线与曲线M相交于A、B两点. 问:△ABC能否为正三角形?若能,求点C的坐标;若不能,说明理由.
某厂生产甲、乙两种产品每吨所需的煤、电和产值如下表所示.
| 用煤(吨) |
用电(千瓦) |
产值(万元) |
|
| 甲产品 |
7 |
20 |
8 |
| 乙产品 |
3 |
50 |
12 |
但国家每天分配给该厂的煤、电有限, 每天供煤至多56吨,供电至多450千瓦,问该厂如何安排生产,使得该厂日产值大?最大日产值为多少?