九（1）班数学兴趣小组经过市场调查，整理出某种商品在第x（1≤x≤90）天的售价与销量的相关信息如下表：
| 时间x（天） |
1≤x＜50 |
50≤x≤90 |
| 售价（元/件） |
x+40 |
90 |
| 每天销量（件） |
200﹣2x |
已知该商品的进价为每件30元，设销售该商品的每天利润为y元．
（1）求出y与x的函数关系式；
（2）问销售该商品第几天时，当天销售利润最大，最大利润是多少？
（3）该商品在销售过程中，共有多少天每天销售利润不低于4800元？请直接写出结果．
将一根长为16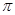
厘米的细铁丝剪成两段，并把每段铁丝围成圆，设所得两圆半径分别为r和R，面积分别为S1和S2．
⑴ 求R与r的数量关系式，并写出r的取值范围；
⑵ 记S＝S1＋S2，求S关于r的函数关系式，并求出S的最小值．
如图，已知△ABC中，∠C＝90°，点D在边AC上，∠BDC＝45°，BD＝10
，AC＝10
，求∠A的度数．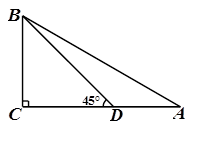
计算：cos245º＋tan60º·sin60º－sin30º．
在四边形ABCD中，对角线AC，BD交于点O，点P是在线段BC上任意一点（与点B不重合），∠BPE＝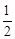
∠BCA，PE交BO于点E，过点B作BF⊥PE，垂足为F，交AC于点G．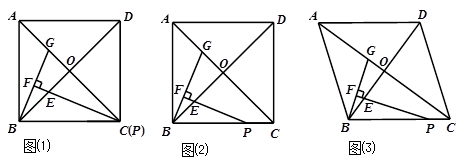
⑴ 若ABCD为正方形，
① 如图⑴，当点P与点C重合时．△BOG是否可由△POE通过某种图形变换得到？证明你的结论；
② 结合图⑵求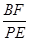
的值；
⑵ 如图⑶，若ABCD为菱形，记∠BCA＝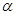
，请探究并直接写出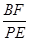的值．（用含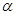的式子表示）
如图，在平面直角坐标系中，直线l：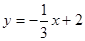
交y轴于点A．抛物线
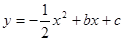的图象过点E（－1，0），并与直线l相交于A、B两点．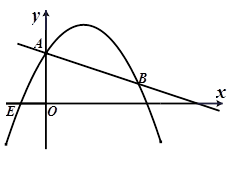
⑴ 求抛物线的解析式；
⑵ 设点P是抛物线的对称轴上的一个动点，当△PAE的周长最小时，求点P的坐标；
⑶ 在x轴上是否存在点M，使得△MAB是直角三角形？若存在，请求出点M的坐标；若不存在，请说明理由．