数学课上，探讨角平分线的作法时，李老师用直尺和圆规作角平分线，方法如下：
作法：①在OA和OB上分别截取OD、OE，使OD= OE；
②分别以点D、E为圆心，大于
DE的长为半径作弧，两弧在∠AOB内交于点C；
③作射线OC．则OC就是∠AOB的平分线，如图①．
小聪只带了直角三角板，他发现利用三角板也可以作角平分线，方法如下：
①利用三角板上的刻度，在OA和OB上分别截取OM、ON，使OM = ON；
②分别过点M、N作OM、ON的垂线，交于点P；
③作射线OP．则OP为∠AOB的平分线，如图②；
小颖的身边只有刻度尺，经过尝试，她发现利用刻度尺也可以作角平分线．
根据以上情境，解决下列问题：
（1）李老师用尺规作角平分线时，用到的三角形全等的判定方法是___________________；
（2）小聪的作法正确吗？请说明理由．
（3）请你帮小颖设计用刻度尺作角平分线的方法（作出图形，写出作图步骤，不予证明）．
如图，已知L1⊥L2，⊙O与L1，L2都相切，⊙O的半径为1cm，矩形ABCD的边AD、AB分别与直线L1，L2重合，∠BCA=600，若⊙O与矩形ABCD沿L1同时向右移动，⊙O的移动速度为2cm，矩形ABCD的移动速度为3cm/s，设移动时间为t（s）．
（1）如图①，连接OA、AC，则∠OAC的度数为 °；
（2）如图②，两个图形移动一段时间后，⊙O到达⊙O1的位置，矩形ABCD到达A1B1C1D1的位置，此时点O1，A1，C1恰好在同一直线上，求圆心O移动的距离（即OO1的长）；
（3）在移动过程中，求当对角线AC所在直线与圆O第二次相切时t的值．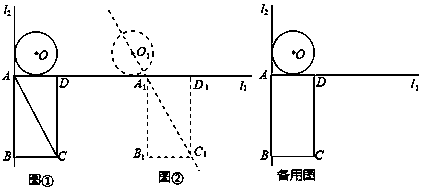
阅读材料：
已知，如图（1），在面积为S的△ABC中，BC=a，AC=b，AB=c，内切圆O的半径为r．连接OA、OB、OC，△ABC被划分为三个小三角形．
∵S=S△OBC+S△OAC+S△OAB=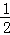
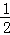BC•r+AC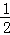•r+AB•r=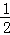（a+b+c）r．
∴r=
．
（1）类比推理：若面积为S的四边形ABCD存在内切圆（与各边都相切的圆），如图（2），各边长分别为AB=a，BC=b，CD=c，AD=d，求四边形的内切圆半径r；
（2）理解应用：如图（3），在等腰梯形ABCD中，AB∥DC，AB=21，CD=11，AD=13，⊙O1与⊙O2分别为△ABD与△BCD的内切圆，设它们的半径分别为r1和r2，求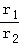
的值．
10月国庆佳节，景山旅行社为吸引游客组团去具有喀斯特地貌特征的黄果树风景区旅游，推出了如下收费标准（如图所示）：
某单位组织员工去具有喀斯特地貌特征的黄果树风景区旅游，共支付给旅行社旅游费用27000元，请问该单位这次共有多少名员工去具有喀斯特地貌特征的黄果树风景区旅游？
已知：
ABCD的两边AB，AD的长是关于x的方程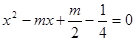
的两个实数根．
（1）当m为何值时，四边形ABCD是菱形？求出这时菱形的边长；
（2）若AB的长为2，那么
ABCD的周长是多少？
已知关于x的方程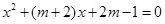
．
（1）求证：方程有两个不相等的实数根；
（2）是否存在实数m，使方程的两个实数根互为相反数?若存在，求出m的值；若不存在，说明理由．