如图1是一个长为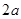 ,宽为
,宽为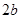 的长方形,沿图中虚线剪开,可分成四块小长方形.
的长方形,沿图中虚线剪开,可分成四块小长方形.
(1)求出图1的长方形面积;
(2)将四块小长方形拼成一个图2的正方形,利用阴影部分面积的不同表示方法,直接写出代数式 、
、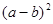 、
、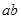 之间的等量关系;
之间的等量关系;
(3)把四块小长方形不重叠地放在一个长方形的内部(如图3),未被覆盖的部分用阴影表示.求两块阴影部分的周长和(用含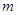 、
、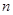 的代数式表示).
的代数式表示).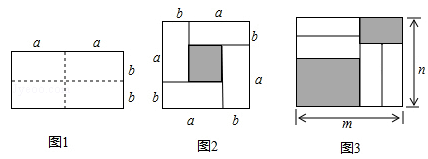
在舞台上有两根竖直放置的铁杆,其中铁杆AB长1m,CD长2m,两根铁杆之间的距离为3m,现在B、D之间拉起一根钢索,杂技演员在上面表演走钢丝,为了描述演员的位置,小明以A点为坐标原点,建立了如图所示的平面直角坐标系,演员的位置为点M,设其横坐标为x,纵坐标为y。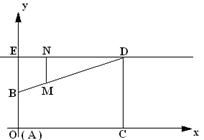
(1)求出线段BD的函数关系式;
(2)为了保护演员的安全,过D点拉了一根与地面平行的钢索DE,在上面挂上了一条保险钢丝MN,MN随演员的移动而移动,并始终垂直于地面,其长度自动调整,设保险钢丝的长度为w,求w与x之间的函数关系式。
若△ABC中∠A=60°,∠B的度数为x,∠C的度数为y,试写出y与x之间的函数关系式,并画出图象。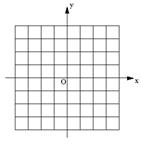
如图,在Rt△ABC中,∠A=90º,AB=6cm,AC=8cm,D、E分别是边AB、AC的中点,点P从点D出发沿DE方向以1cm/s的速度运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R、交DE于G,当点Q与点C重合时,点P停止运动.设点P运动时间为ts.
(1)点D到BC的距离DH的长是 ;
(2)当四边形BQGD是菱形时,t= ,S△EGR= ;
(3)令QR=y,求y关于t的函数关系式(不要求写出自变量的取值范围);
(4)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的t的值;若不存在,请说明理由.
如图,点O是边长为8的正方形ABCD边AD上一个动点(4<OA<8),以O为圆心、OA长为半径的圆交边CD于点M,连接OM,以CM为边在正方形ABCD内部作∠CMN=∠DOM,直线MN交边BC于点N.
(1)试说明:直线MN是⊙O的切线;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O运动的过程中,设△CMN的周长为p,试用含x的代数式表示p,你有什么发现?
某饰品店老板去批发市场购买新款手链,第一次购手链共用100元,回来后该手链按定价2.8元销售,并很快售完.由于该手链深得“潮女”喜爱十分畅销,第二次去购手链时,每条的批发价已比第一次高0.5元,共用去了150元,所购数量比第一次多10条.当这批手链售出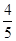 时,出现滞销,便以定价的5折售完剩余手链.(手链销售中不考虑其它因素)
时,出现滞销,便以定价的5折售完剩余手链.(手链销售中不考虑其它因素)
(1)求第一次该手链的批发价;
(2)试问该老板第二次销售手链是赔钱了,还是赚钱了?用数据说明.