(本小题满分10分)在甲、乙两个盒子中分别装有标号为1,2,3,4的四个球,现从甲、乙两个盒子中各取出1个球,每个球被取出的可能性相等.
(1)求取出的两个球上标号为相同数字的概率;
(2)求取出的两个球上标号之积能被3整除的概率.
(本题满分15分)
已知三次函数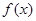 的最高次项系数为a,三个零点分别为
的最高次项系数为a,三个零点分别为 .
.
⑴ 若方程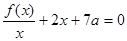 有两个相等的实根,求a的值;
有两个相等的实根,求a的值;
⑵若函数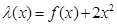 在区间
在区间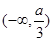 内单调递减,求a的取值范围.
内单调递减,求a的取值范围.
(本题满分14分)在三棱柱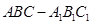 中,
中,
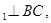
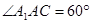 ,
,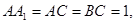
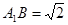
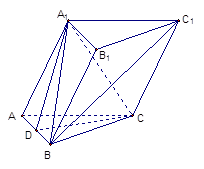
⑴求证:平面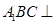 平面
平面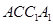 ;
;
⑵如果D为AB的中点,求证: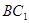 ∥平面
∥平面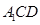
(本题满分14分)在平面直角坐标系 中,点
中,点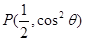 在角
在角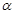 的终边上,点
的终边上,点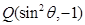 在角
在角 的终边上,且
的终边上,且
⑴求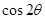 的值;⑵求
的值;⑵求 的值。
的值。
已知曲线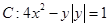
(I)若直线 与曲线
与曲线 只有一个公共点,求实数
只有一个公共点,求实数 的取值范围;
的取值范围;
(II)若直线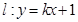 与曲线
与曲线 恒有两个不同的交点
恒有两个不同的交点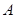 和
和 ,且
,且 (其中
(其中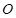 为坐标原点),求实数
为坐标原点),求实数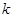 的取值范围。
的取值范围。
(本小题满分12分)已知椭圆的两个焦点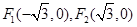 ,且椭圆短轴的两个端点与
,且椭圆短轴的两个端点与 构成正三角形
构成正三角形
(I)求椭圆的方程;
(Ⅱ)过点(1,0)且与坐标轴不平行的直线 与椭圆交于不同两点P、Q,若在
与椭圆交于不同两点P、Q,若在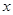 轴上存在定点E(
轴上存在定点E(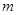 ,0),使
,0),使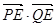 恒为定值,求
恒为定值,求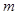 的值.
的值.