某工厂去年新开发的某产品的年产量为100万只，每只产品的销售价为10元，固定成本为8元．今年，工厂第一次投入100万元的科技成本，并计划以后每年比上一年多投入100万元，预计产量每年递增10万只，投入n次后，每只产品的固定成本为g（n）＝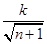
（k为常数，n∈Z且n≥0）．若产品销售价保持不变，第n次投入后的年纯利润为f（n）万元（年纯利润＝年收入－年固定成本－年科技成本）．
（1）求k的值，并求出f（n）的表达式；
（2）问从今年起，第几年纯利润最高？最高纯利润为多少万元？
汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表（单位：辆）：
| 轿车A |
轿车B |
轿车C |
|
| 舒适型 |
100 |
150 |
Z |
| 标准型 |
300 |
450 |
600 |
按类用分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆.
(1)求z的值；
(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；（用列举法求概率）
(3)用随机抽样的方法从B类舒适型轿车中抽取8辆，经检测它们的得分如下：9.4，8.6，9.2，9.6，8.7，9.3，9.0，8.2.把这8辆轿车的得分看成一个总体，从中任取两个数，求两数之差的绝对值不超过0.5的概率.（用列举法求概率）
一个盒中有6个球，其中红球1个，黑球3个，白球2个，现从中任取3个球，用列举法求下列事件的概率：（1）求取出3个球是不同颜色的概率.（2）恰有两个黑球的概率（3）至少有一个黑球的概率
为了迎接世博会，某旅游区提倡低碳生活，在景区提供自行车出租。该景区有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元。根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超出6元，则每超过1元，租不出的自行车就增加3辆。为了便于结算，每辆自行车的日租金x（元）只取整数，并且要求出租自行车一日的总收入必须高于这一日的管理费用，用y（元）表示出租自行车的日净收入（即一日中出租自行车的总收入减去管理费用后的所得）。
（1）求函数
的解析式及其定义域；
（2）试问当每辆自行车的日租金定为多少元时，才能使一日的净收入最多？
已知
, 若
在区间
上的最大值为
, 最小值为
, 令
.
(I) 求
的函数表达式；
(II) 判断的单调性, 并求出的最小值.
已知函数
（1）求函数
的值域；
（2）若
时，函数的最小值为
，求
的值和函数的最大值。