为了迎接世博会,某旅游区提倡低碳生活,在景区提供自行车出租。该景区有50辆自行车供游客租赁使用,管理这些自行车的费用是每日115元。根据经验,若每辆自行车的日租金不超过6元,则自行车可以全部租出;若超出6元,则每超过1元,租不出的自行车就增加3辆。为了便于结算,每辆自行车的日租金x(元)只取整数,并且要求出租自行车一日的总收入必须高于这一日的管理费用,用y(元)表示出租自行车的日净收入(即一日中出租自行车的总收入减去管理费用后的所得)。
(1)求函数 的解析式及其定义域;
的解析式及其定义域;
(2)试问当每辆自行车的日租金定为多少元时,才能使一日的净收入最多?
(本小题满分10分)选修4-5:不等式选讲:
已知函数 .
.
(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于 的不等式
的不等式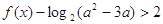 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分10分)选修4-4:坐标系与参数方程:
以直角坐标系的原点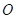 为极点,
为极点,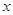 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线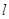 的参数方程为
的参数方程为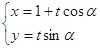 (
(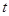 为参数,
为参数, ),曲线
),曲线 的极坐标方程为
的极坐标方程为 .
.
(Ⅰ)求曲线 的直角坐标方程;
的直角坐标方程;
(Ⅱ)设直线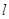 与曲线
与曲线 相交于
相交于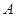 、
、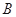 两点,当
两点,当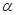 变化时,求
变化时,求 的最小值.
的最小值.
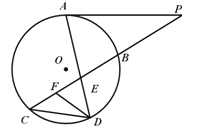
(本小题满分10分)选修4-1:几何证明选讲:
如图所示,已知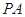 与⊙
与⊙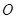 相切,
相切,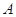 为切点,过点
为切点,过点 的割线交圆于
的割线交圆于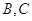 两点,弦
两点,弦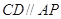 ,
,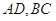 相交于点
相交于点 ,
, 为
为 上一点,且
上一点,且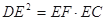 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求
,求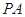 的长.
的长.
(本小题满分12分) 设函数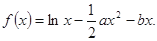
(1)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(2)令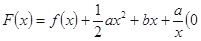 <
< ≤
≤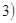 ,其图像上任意一点
,其图像上任意一点 处切线的斜率
处切线的斜率 ≤
≤ 恒成立,求实数
恒成立,求实数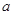 的取值范围;
的取值范围;
(3)当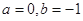 时,方程
时,方程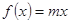 在区间
在区间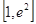 内有唯一实数解,求实数
内有唯一实数解,求实数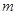 的取值范围.
的取值范围.
(本小题满分12分)椭圆 :
: 的离心率为
的离心率为 ,长轴端点与短轴端点间的距离为
,长轴端点与短轴端点间的距离为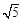 .
.
(1)求椭圆 的方程;
的方程;
(2)设过点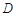
 的直线
的直线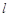 与椭圆
与椭圆 交于
交于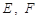 两点,
两点, 为坐标原点,若
为坐标原点,若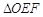 为直角三角形,求直线
为直角三角形,求直线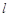 的斜率.
的斜率.