(本小题满分10分)选修4-1:几何证明选讲:
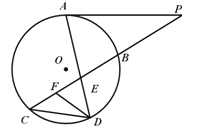
如图所示,已知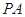 与⊙
与⊙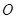 相切,
相切,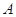 为切点,过点
为切点,过点 的割线交圆于
的割线交圆于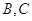 两点,弦
两点,弦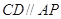 ,
,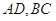 相交于点
相交于点 ,
, 为
为 上一点,且
上一点,且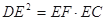 .
.
(Ⅰ)求证: ;
;
(Ⅱ)若 ,求
,求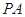 的长.
的长.
设函数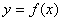 是定义在
是定义在 上的减函数,并且满足
上的减函数,并且满足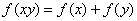 ,
,
(1)求 ,
,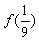 ,
, 的值,(2)如果
的值,(2)如果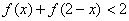 ,求x的取值范围。
,求x的取值范围。
已知函数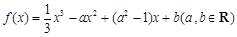
(1)若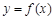 的图象在点
的图象在点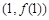 处的切线方程为
处的切线方程为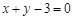 ,求
,求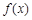 在区间
在区间 上的最大值;
上的最大值;
(2)当 时,若
时,若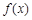 在区间
在区间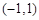 上不单调,求
上不单调,求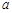 的取值范围.
的取值范围.
已知椭圆的一个顶点为A(0,-1),焦点在x轴上,若右焦点到
直线 的距离为3。
的距离为3。
(1)求椭圆的方程;
(2)设直线 与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的
与椭圆相交于不同的两点M,N,当|AM|=|AN|时,求m的
取值范围.
已知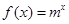 (m为常数,m>0且m≠1).
(m为常数,m>0且m≠1).
设 (n∈
(n∈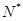 )是首项为m2,公比为m的等比数列.
)是首项为m2,公比为m的等比数列.
(1)求证:数列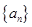 是等差数列;
是等差数列;
(2)若 ,且数列
,且数列 的前n项和为Sn,当m=2时,求Sn;
的前n项和为Sn,当m=2时,求Sn;
如图,在三棱锥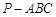 中,
中,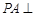 平面
平面 ,
,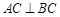 ,
, 为
为
侧棱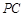 上一点,它的正(主)视图和侧(左)视图如图所示.
上一点,它的正(主)视图和侧(左)视图如图所示.
(1)证明: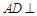 平面
平面 ;
;
(2)求三棱锥 的体积;
的体积; 