(本小题满分12分)数列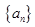 中,已知
中,已知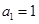 ,
, 时,
时, .数列
.数列 满足:
满足: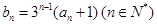 .
.
(Ⅰ)证明: 为等差数列,并求
为等差数列,并求 的通项公式;
的通项公式;
(Ⅱ)记数列 的前
的前 项和为
项和为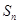 ,是否存在正整数
,是否存在正整数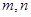 ,使得
,使得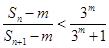 成立?若存在,求出所有符合条件的有序实数对
成立?若存在,求出所有符合条件的有序实数对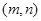 ;若不存在,说明理由.
;若不存在,说明理由.
(本小题12分) 已知函数 ,
, .
.
(1)求函数 的周期和最大值;
的周期和最大值;
(2)设函数 在
在 的区间上的图像与
的区间上的图像与 轴的交点从左到右分别为
轴的交点从左到右分别为 ,图像的最高点为
,图像的最高点为 ,求
,求 与
与 的夹角
的夹角 的余弦值.
的余弦值.
(本小题12分)2014年2月,西非开始爆发埃博拉病毒疫情,埃博拉病毒是引起人类和灵长类动物发生埃博拉出血热的烈性病毒,引发了世界恐慌。中国国际救援组织立即采用分层抽样的方法从病毒专家、心理专家、地质专家三类专家中抽取若干人组成研究团队赴西非工作,有关数据见表1(单位:人).
病毒专家为了检测当地群众发烧与是否更易受博拉病毒疫情影响,在当地随机选取了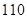 群众进行了检测,并将有关数据整理为不完整的
群众进行了检测,并将有关数据整理为不完整的 列联表(表2).
列联表(表2).
表1:
| 相关人员数 |
抽取人数 |
|
| 病毒专家 |
48 |
 |
| 心理专家 |
24 |
 |
| 地质专家 |
72 |
6 |
表2:
| 发烧 |
无发烧 |
合计 |
|
| 患Ebola |
50 |
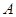 |
60 |
| 不患Ebola |
 |
40 |
50 |
| 合计 |
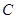 |
 |
 |
(1)求 ;
;
(2)写出表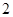 中
中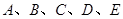 的值,并判断是否有99.9%的把握认为疫情地区的群众发烧与患Ebola病毒有关;
的值,并判断是否有99.9%的把握认为疫情地区的群众发烧与患Ebola病毒有关;
(3)若从研究团队的病毒专家和心理专家中随机选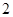 人撰写研究报告,求其中恰好有
人撰写研究报告,求其中恰好有 人为病毒专家的概率.
人为病毒专家的概率. 临界值表:
临界值表:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
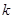 |
2.072 |
2.706 |
3.841 |
5.024 |
6. 635 |
7.879 |
10.828 |
(本小题12分)在等差数列 中,
中,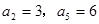 ..
..
(1)求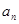 ;
;
(2)设 ,求数列
,求数列 的前
的前 项和
项和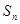 的取值范围.
的取值范围.
(本小题满分14分)已知函数
(Ⅰ)求函数 的定义域;
的定义域;
(Ⅱ)确定函数 在定义域上的单调性,并证明你的结论;
在定义域上的单调性,并证明你的结论;
(Ⅲ)若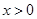 时
时 恒成立,求正整数
恒成立,求正整数 的最大值.
的最大值.
(本小题满分14分)如图,已知椭圆 的离心率为
的离心率为 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点 为顶点的三角形的周长为
为顶点的三角形的周长为 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设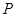 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线 和
和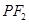 与椭圆的交点分别为
与椭圆的交点分别为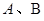 和
和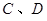 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线 、
、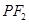 的斜率分别为
的斜率分别为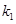 、
、 ,证明
,证明 ;
;
(Ⅲ)探究 是否是个定值,若是,求出这个定值;若不是,请说明理由.
是否是个定值,若是,求出这个定值;若不是,请说明理由.