(本小题满分16分)设函数f(x)=x2-2tx+2,其中t∈R.
(1)若t=1,求函数f(x)在区间[0,4]上的取值范围;
(2)若t=1,且对任意的x∈[a,a+2],都有f(x)≤5,求实数a的取值范围.
(3)若对任意的x1,x2∈[0,4],都有|f(x1)-f(x2)|≤8,求t的取值范围.
对正整数
,记
,
.
(1)求集合
中元素的个数;
(2)若
的子集
中任意两个元素之和不是整数的平方,则称
为"稀疏集".求
的最大值,使
能分成两个不相交的稀疏集的并集.
如图,椭圆的中心为原点
,长轴在
轴上,离心率
,过左焦点
作
轴的垂线交椭圆于
、
两点,
.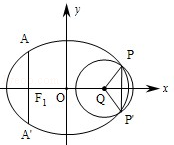
(1)求该椭圆的标准方程;
(2)取垂直于
轴的直线与椭圆相交于不同的两点
、
,过
、
作圆心为
的圆,使椭圆上的其余点均在圆
外.若
,求圆
的标准方程.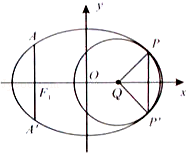
在
中,内角
的对边分别是
,且
.
(1)求
;
(2)设
,
,求
的值.
如图,四棱锥
中,
,
,
,
,
为
的中点,
.
(1)求
的长;
(2)求二面角
的正弦值.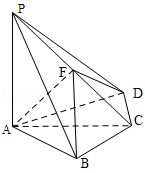
某商场举行的"三色球"购物摸奖活动规定:在一次摸奖中,摸奖者先从装有3个红球与4个白球的袋中任意摸出3个球,再从装有1个蓝球与2个白球的袋中任意摸出1个球,根据摸出4个球中红球与蓝球的个数,设一、二、三等奖如下:
| 奖级 |
摸出红、蓝球个数 |
获奖金额 |
| 一等奖 |
3红1蓝 |
200元 |
| 二等奖 |
3红0蓝 |
50元 |
| 三等奖 |
2红1蓝 |
10元 |
其余情况无奖且每次摸奖最多只能获得一个奖级.
(1)求一次摸奖恰好摸到1个红球的概率;
(2)求摸奖者在一次摸奖中获奖金额
的分布列与期望
.